THE DANGERS OF ANALOGIES

by Donald E. Simanek

Here's a statement of teaching philosophy on a physics job application:

The use of analogies from everyday life helps students to understand concepts better, to realize that it is mostly the same physical arguments that explain phenomena they see around them.

This applicant was not chosen by us.

Job seekers who are tempted to include with their resumes a statement of their teaching philosophy ought to write it from experience, not from speculation. It might be read by people who have been in the ed-biz for very many years, who have seen the educational fad pendulum swing through several cycles, who have seen each new utopian educational panacea end up as a dismal failure in the real world. One thing remains constant in education: Nothing works if the students don't work.

The notion is widespread among teachers, especially at the introductory levels of physics, that use of analogies to get across concepts is a "good thing." Actually, I (who have taught both introductory and advanced courses) think that it's a very risky practice, which usually leads to concepts, ideas and thinking habits that must later be painfully unlearned.

Analogies compare two things that have no logical or physical relation to each other.

First let's define "analogy". We often compare one thing with another as an illustrative device, or to conjure up a mental picture of something not easily visualized. Such a comparison may even help us remember things—sort of a mnemonic device. The comparison is generally between two things that have no logical or physical relation to each other. This may be called a "benign analogy" since is has some slight usefulness, and is not taken seriously enough to do harm to one's thinking. In fact, psychologists observe that the more outrageous or illogical the comparison is, the easier it is to remember as a mnemonic device.

Then there's the far more sinister "argument by analogy" in which a comparison is invoked in order to derive a conclusion. It takes the form "Because M has properties A, B and C, then if N has properties A and B, it also has C." Stated in this stark way, its absurdity as a "method of argument" is obvious, for it can be used to conclude things that are patently false. The dangers of thinking by analogy are noted by nearly every book on logic, argument, and debate. For example, chapter 8, "Pitfalls of Analogy" in the Robert H. Thouless classic, Straight and Crooked Thinking, 1932 (later rewritten and reprinted as How to Think Straight).

When an analogy is used as a "homely example", memory crutch, poetic metaphor, colorful illustration, or with humorous or satirical intent, and is understood as such by the reader or listener, it probably is benign. But analogies should never be used as arguments to reach a conclusion, and should never substitute for reason and logic. The examples we will discuss are those that are harmful in physics teaching because they encourage lazy and sloppy habits of thought.

Common analogies in physics teaching.

Let's list some of those analogies commonly presented in introductory physics courses:

The "soldier" analogy of refraction at an interface between media of different refractive index. There's also the "wheel and axle" demonstration used as an analogy. I first saw this as an undergraduate in the 1950's and naively supposed that it had passed out of fashion. Not so! It appears in Douglas C. Giancoli's text [Physics, 3rd ed., Prentice-Hall 1991, Fig 11-28]. The caption even describes it as "Soldier analogy to derive law of refraction for waves."

The soldiers are marching from firm ground (medium 1) into mud (medium 2) and hence are slowed down. The soldiers that reach the mud first are slowed down first and the row bends as shown in Fig. 11-28a. Let us consider the wave front (or row of soldiers) labeled A in Fig 11-28b. In the same time t that A₁ moves a distance d₁ = v₁t we see that A₂ moves a distance d₂ = v₂t. The two triangles shown have the side labeled a in common. Thus

d₁ v₁ t sin θ = —— = ———— 1 a a

and

d₂ v₂ t sin θ = —— = ———— 2 a a

Dividing these two equations, we find that

sin θ₂ v₂ —————— = ———
[11-16]
sin θ₁ v₁

since θ₁ is the angle of incidence, and θ₂ is the angle of refraction, Eq. 11-16 gives the quantitative relation between the two.

Anyone who has been in a marching band will find this argument rather unconvincing. Only a poorly trained marching band will refract on crossing the interface between astroturf and blacktop. Bands are trained to maintain a constant stride whatever the terrain. Does this analogy give any correct insight about the underlying mechanism of light refraction? If the marching band crossed a curved interface, would the ranks focus to a point, or diverge in many directions? Does the analogy work for reflection? (Imagine a marching band undergoing total internal reflection at the stadium wall!) If only one marching file were present, would refraction occur? Probably not. The reason a well-trained marching group maintains straight ranks is because marchers are taught to "guide right". If a very narrow beam of light falls on an interface, it still refracts. There's nothing analogous to "guiding right" on the rest of the wave front in the case of light.

This reveals an underlying and unstated assumption lurking in this pseudo-explanation. Why doesn't a file of marchers continue in a straight line, but with reduced stride in the rougher ground? Why does an individual marcher change direction at the interface? If all marchers did continue in a straight line, there'd be no refraction, but the ranks would no longer be perpendicular to the files. The explanation expects the reader to assume that the necessary adjustments will be made to maintain perpendicularity between ranks and files. And what is the explanation for that? These are the sorts of questions the inquiring student should ask of any purported "explanation". If such questions are raised about the usual pedagogical analogies they expose the analogies' inadequacies.

But doesn't this analogy at least get across the correct idea that it's the relative speed in the two media that is the cause of refraction, and the determiner of the refraction angle? Doesn't it also correctly motivate the geometric/mathematical analysis, and, more importantly (to students), to "get" the "right" answer?

Maybe; but at what cost? In Giancoli's treatment the cost is the use of an unstated, unproven and unmotivated assumption: that each soldier changes his or her direction of march immediately on crossing the boundary so that they all march exactly perpendicular to the "wave fronts." Giancoli is assuming the refraction that he's "deriving"! The whole argument (which occupies a page in his book) collapses into a circular argument!

To see how the unstated assumption matters, consider a slightly different assumption. Suppose that the soldiers do change their stride on crossing the boundary, but maintain their straight files. They don't change the direction of their march. The ranks will still refract, though the ranks will not be perpendicular to the direction of march. This effect is often observed in poorly trained marching units. In this case, the derivation yields the result:

tan θ₂ v₂ —————— = ——— tan θ₁ v₁

Not exactly the desired equation! (The two results are identical in the limit of small angles, but that's small consolation.)

This is all reminiscent of the difficulties Descartes had when trying to derive the law of refraction with even homelier analogies of a tennis ball bursting through a flimsy net. Textbook authors today too often show an ignorance of the historical precedents for their mistakes. [1] They keep reinventing the square wheel.

The wheel and axle refraction occurs for two reasons: (a) slowing of the wheel due to friction, and (b) "guiding" by the axle. A single wheel encountering a very rough medium would also refract, but for a different reason (and according to a different law). That 'refraction' results from a torque of the rougher medium acting on one side of the wheel earlier than the other side. If you make such a wheel, say from Meccano or Erector parts, or use a toy truck, you'll find that the refraction is a lot more complicated than you thought, and not at all like that for light. It also depends on whether the two wheels are fastened to the axle, or whether they are free to rotate on the axle.

Does any of this help one understand light? Does it give the correct formula for refraction? Does it predict total internal reflection? For that matter, does either refraction analogy predict that both reflection and reflection occur simultaneously at an interface? No.

These analogies of refraction fail on nearly every one of our criteria.

Bent soda straw.

This demonstration is sometimes used to illustrate refraction. A soda straw in a glass seems to be "bent" at the water surface. This looks something like the ray diagram of refraction seen in many textbooks. Is it refraction that causes the "bending" and the discontinuity of the straw's image at the water surface? Yes, but it's a bit more complicated. The student may think that this only illustrates refraction at the water's upper surface.

If you look carefully there's a size difference between the two portions of the straw. Also there may be a break in straw position at the surface. What's really happening is that the cylindrical glass and the water inside act as a cylindrical lens. The refraction causing this appearance is not due to light refracting at the upper surface, but due to refraction at the curved sides of the glass.

This is a case where a demonstration, or a picture, can mislead if not carefully explained.

The "picket fence and rope" analogy of light transmission through polarizers.

This analogy assumes that polarizers are something like the parallel slats of a picket fence. Light is something like a stretched rope that you shake up and down to create a wave. If the wave passes through the slots of a picket fence, it can move up and down (if the fence slats are oriented vertically) but not if they are horizontal. Now have the rope pass through a section of fence with vertical slats, and also another section with horizontal slats. The rope wave can't get through both, whether it is vibrating up/down or right/left. You still see this crude analogy, with pictures, in many books.

Typical textbook picket fence analogy.

Light passing through crossed and uncrossed polarizers.

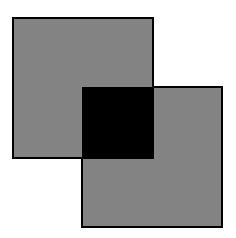
What's wrong with this analogy? Almost everything! For one thing, it's a one-case explanation. Put two polarizers on an overhead projector, one on top of the other with axes parallel. Light passes through both with modest diminution of intensity (actually considerable diminution, but our eyes tend not to notice). Then rotate either polarizer 90° so their axes are perpendicular. Light is now blocked. Now ask students what will happen if a third polarizer is placed between the other two, with its axis at 45° to the other two. Does the picket fence analogy help students get the right answer? No, and when you perform the experiment, they are very surprised. Their 'learning' of the 'explanation' was useless to them. They had only an illusion of understanding, and worse, they were confident of their wrong understanding.

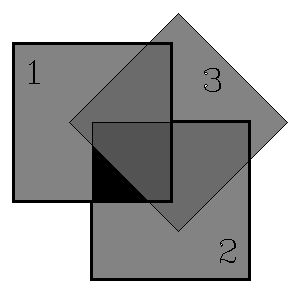Two polarizers, axes parallel.	Two polarizers, axes perpendicular.	Two polarizers, 1 and 2 with perpendicular axes, and third polarizer between them, axis at 45° to the other two.

This drawing simulates what is seen. A single polarizer looks gray, for it only transmits about 40% of the light intensity. Two polarizers with crossed (perpendicular axes) transmit very little light intensity (nearly black). But if a third polarizer is placed between two crossed ones, considerable light intensity does get through.

The "picket-fence and rope" analogy isn't presented quantitively, and I see no way to make it quantitative to correctly describe the picket fence and rope experiment and also match experimental results with polarizers. You'd have to do a lot of hand waving (or rope waving) to do that. The picket fence and rope is not a good analogy for the molecular structure of polarizers, nor of the way light interacts with that structure. Nor does the analogy include the photon nature of light itself. On a practical level, the analogy wouldn't help us predict the colors produced when a sheet of cellophane is placed between the polarizers.

I think this example, better than most others, points out the real dangers of analogies in education. Yet students like analogies, teachers tell me. Students 'feel' that they have gotten some understanding when an analogy is presented glibly. I submit that it's not just students who are susceptible to the lure of metaphors and analogy. It may be one of the many counterproductive human tendencies that we ought to try to overcome (i.e., try to understand them, put them in their place, and not use them inappropriately).

In case you haven't done the polarizer experiment: The third polarizer between the crossed ones causes light to pass through where the two crossed ones alone blocked it. A vector model of light intensity gives a fairly useful classical model, but breaks down when you try to consider the atomic-molecular nature of the polarizer and the quantum nature of the light. The picket-fence analogy doesn't help you understand what the photons are doing when they encounter molecules.

Now how many times has this polarizer experiment been described in textbooks, demonstrated by teachers, and done by students, with only two polarizers? Even if a third polarizer is lying nearby, how many will think to try it between the others? What has happened to curiosity, to the experimental method? The analogy 'seems' complete enough to most students (and some teachers) that there's no need to investigate it in new ways! For me this is another example that most of education is a sham and a fraud, unable even to achieve its own stated goals—except for those few students who manage to achieve an education in spite of their schooling.

Comment: Has anyone ever actually made the polarizer analogy work with a real rope and a real picket fence, and with the polarization plane of the incident light at, say, an angle of 45° to the slats of the first picket fence? The rope is a classical analogue of polarization, of no help in understanding the quantum model of polarization.

Comment: In the diagram above the unpolarized light is represented by a figure with a lot of vectors going in all directions. This, too, can be misleading if not explained. This conventional symbol is merely an icon to indicate that the light's photons are polarized in many directions in an unbiased manner, any direction being equally probable. It does not indicate that these vectors should be summed (for they would add to zero.)

The hydraulic analogy of electric currents.

Most students I have encountered think they appreciate the analogy, but it doesn't help them because they haven't fully understood hydraulic systems. Ask them a question such as this, to see whether they understand it correctly:

Consider a steady DC current, with the electrons moving through a resistor in a circuit. The average speed of the electrons coming out of the resistor is _____ the average speed they had entering the resistor. (a) greater than (b) smaller than (c) the same as

The answer is (c). The average kinetic energy is the same going out as in. After all, Kirchoff's laws, which students claim to "know," require that the current be the same on either side of the resistor, and charge is not created or destroyed in the resistor, so what goes in, comes out. It's electrical potential energy that's converted to thermal energy. Now ask students how this works in hydraulics, when water flows through a section of pipe filled with a water filter (resistor). The input and output pipe cross sectional areas are the same. Again, the water speed in and out is the same, it's the potential energy associated with the pressure difference across the filter that's converted to thermal energy.

Much of education is cleverly contrived not to produce understanding, but merely the ILLUSION of understanding.

The resistor warms up, indicating that electrical energy is converted to thermal energy. This energy comes from the battery, of course. So what do the electrons have to do with the transfer of energy from battery to resistor? Can they be considered "carriers" of energy? If not, what is?

Yes, the electrons are carriers, just as a line of automobiles at rush hour going at constant speed down a hill must lose the potential energy they gain from going downhill by applying their brakes, converting that potential energy to thermal energy. [Whoops! An analogy!]

The analogy between water waves (in a ripple tank) and light waves.

This is a fairly harmless analogy. Many classical light phenomena are demonstrable in a mathematically correct way using water waves, but with some obvious exceptions:

The water waves have only one polarization direction.
The water waves require a medium, light doesn't.
In the essentially two-dimensional ripple tank, the wave energy propagates by an inverse first power law, not an inverse square law. [2]
The water waves are rapidly damped; light waves usually aren't.
The water waves have no good analogy with photons.

Comparison of magnetic "poles" to point charges.

When I took freshman physics the magnetic pole strength was defined, and the equation written:

m₁ m₂ F = c ————— , in cgs units, c = 1. r²

If F is in dynes, r in cm, and m in "unit poles", then c = 1. We even did a laboratory exercise exploring this relation quantitatively.

Iron filings and bar magnet show field lines.

This isn't done anymore, because as a magnet and iron filings clearly show, the "poles" of a magnet are not localized very well, so it's hard to find r precisely.

Field lines. In the same course we were "taught" that from each unit charge came 4π field lines. On hearing this I wondered, "who counted them?" Then I realized you can't count 4π, and was convinced that the physics teacher, and the textbook, were rather careless in their use of language. Later when we got to motors and generators we heard a lot about "cutting field lines," and wondered if they snapped like rubber bands when you cut them. After all, our professor had said that at one time fields were thought of as elastic strain in the ether, but that physicists no longer believed in the ether.

Are analogies ever useful in scientific discovery?

You may ask, "Don't analogies often play a useful role in science, at least in the early stages of concept formation, and in the preliminary models used to describe new phenomena?

Yes, one can cite a number of historical examples of analogies that paved the way to new understanding. It's a mixed bag. In my view some analogies may have been productive in the early stages of model formation, but became a hindrance later on, especially when they were held too long. The picture is also biased by the selective memory of history. We remember and recount the successful examples, and sweep the failures under the rug. Here are a few cases worth considering:

Galileo argued that the four moons of Jupiter were analogous to the Copernican model of the solar system. He had no more argument than that to go on, for the celestial mechanics of Kepler and Newton were not yet available. Galileo's critics were entirely justified in dismissing the force of this analogy, but they were guilty of even more blatant analogies in their own arguments.

Kepler's harmony of the spheres associating a tune with each planet.	Kepler's solar system model with nested spheres and Pythagorean solids.

Johannes Kepler was led astray many times in his search for a planetary model by arguments from analogy. Examples: The music of the spheres. The Sun as a magnet. The spheres nested with pythagorean solids. Kepler didn't formulate his famous three laws of planetary motion until he abandoned all of these and devised a purely mathematical model.
Much of the problem with the luminiferous ether was due to people arguing that light must be analogous to sound and other "material" waves. "Light must have something to 'wave' in." This now-abandoned ether idea was firmly believed by physicists for well over thirty years.
The early forms of the Bohr model of the atom were presented in textbooks by analogy with the solar system. Some early textbooks showed precessing orbits of electrons. The deficiencies of this analogy are spelled out in most atomic and nuclear texts, and include: (1) inconsistency of a deterministic orbit with the uncertainty principle, (2) the fact that the accelerating electron in a circular orbit does not radiate away energy, and (3) how can the orbit of a zero angular momentum state pass right through the nucleus?

Harmless pedagogical analogies?

I have frequently challenged physics teachers to tell me how well a student could do on their exams if the student understood nothing, but had eidetic imagery, the ability to memorize anything perfectly. Could that student pass the course? Rarely does any teacher assure me that such a student would flunk. There are a few relatively harmless analogies in physics teaching.

The mousetrap and cork demo illustrating a nuclear chain reaction.

For those who haven't seen it, this demo has a large plexiglass or wire mesh cage in which there are many mousetraps filling the bottom, all set to spring, with two corks on each. A cork is tossed in the cage, which may spring a trap. If if doesn't, another is tossed in until one trap is sprung, and its corks will go flying and fall on other traps, springing them. A chain reaction of flying corks and bouncing mousetraps ensues. The action is over in a short time, leaving a jumbled mess to be painstakingly reset for the next class demo. The analogy is to a fissioning atom giving off (on average) two neutrons, which trigger other atoms to fission in a chain reaction.

Comments: To compare mousetraps and corks to atoms and neutrons is obviously a huge stretch. Also the detailed physical processes of springing the trap and the bouncing of corks from the cage have no counterpart in atoms. Yet I see very little harm arising from this demo. No student is likely to generalize it too far. Its value is almost entirely mnemonic. No physics is learned from it.

Then there's the observation that in many cases traps are sprung not by flying corks, but by one mousetrap (atom) falling on another mousetrap. Is there any counterpart of this in nuclear fission in an atomic bomb?

The cascaded electrical filter analogy of musical wind instruments, such as the recorder, flute, clarinet.

This was used by Helmholtz and became a standard presentation in books on musical acoustics. It is seldom seen in elementary books. A student who knows enough electrical theory and has enough mathematics to calculate electrical networks will probably take the analogy in the right spirit and not be harmed by it.

Microwave diffraction simulation of X-ray crystal diffraction. This is a standard laboratory experiment. A crystal is simulated by a regular array of steel bearings in a styrofoam block about a foot square. Microwaves are scattered from the model crystal and detected by a rotatable detector. The crystal and detector may both be rotated. Angles of strong diffraction are recorded and used to infer the geometry of the array of scatterers. Though it is an analogy of geometry: pattern and scale. It is highly instructive and a lot less expensive than an X-ray system. It is not, however, a teaching analogy, and I've never seen it in a textbook.

Tests an analogy should meet:

The analogy should compare the unfamiliar to the already familiar. The analogy of currents to the flow of water in pipes is useless unless the student already has a good grasp of hydraulics.
The analogy should be simple and easy to present. If the comparison requires elaborate justification or explanations, forget it. If the analogy requires a long list of "exceptions" and qualifications, the time would be better spent on a direct and fuller physical and mathematical treatment.
The analogy should be reasonably complete in all important details. The non-analogous details shouldn't require elaborate explanation.
The analogy should be mathematically analogous. The two cases being related ought to obey the very same mathematical equations without exception.
The analogy should be physically analogous. The physical principles in the cases being compared ought to also be meaningfully analogous.
Analogies ought never be represented as a demonstrations, arguments, or proofs. Analogies must never replace rigorous mathematical and physical development.
The analogy should not be restricted to a single case or a special case.
All obvious extrapolations of the analogy should be valid. The analogy should continue to give correct predictions for other cases that will occur later in the course, and for other cases that a thoughtful student might apply it to.
There should be no hidden or unstated assumptions required to make the analogy "work."

Finally:

Don't let students take analogies seriously. Don't let students get in the habit of using analogies as mental "crutches." Our goal should be "Throw away your crutches."

Most students prefer their abstractions cast in concrete. — Piaget's lost principle.

Visual analogies.

Visualization is also an analogy, which students often use as a crutch. Pictures we draw of atoms, wave functions, etc., are always incomplete and potentially misleading. One of the difficulties students have with advanced physics is that they have become dependent on visual models. When they encounter physics that can't be visualized, and for which pictures can't be drawn, they experience severe cognitive dissonance. This is when they consider majoring in something simpler and more concrete.

My sophomore-level students were shocked into absolute intellectual impotence when, in a classical mechanics class, I asked them to find the volume and area of a four-dimensional sphere, and even suggested they might go to higher dimensions. They had taken the standard calculus sequence, but apparently hadn't learned it well enough to do anything with calculus. They claimed that they understood how we set up the integrations over round objects in two and three dimensions when I'd done them in class, but they couldn't extend the methods to four dimensions. Questioning revealed that they didn't even try very seriously because they couldn't figure out how to draw a picture of a four dimensional object! I suggested they do it without drawing pictures. They couldn't believe that I was serious. Well, don't we often tell Freshmen that the first step in working a problem is to "draw a picture?"

Before we draw any picture we should remember that it is another dangerous analogy!

Based on these criteria, are there any analogies that are useful and "safe" in teaching physics. No, I don't know of any. If you can come up with one, please get in touch. I'd also appreciate correspondence on other analogies that cause trouble. [3]

Mathematical analogies.

Can we teach physics without ever using analogy? Let's not forget that mathematical models are analogies. And even these carry some dangers, for mathematical models are inevitably incomplete, incorrect and only as good as the data that went into them. Albert Einstein recognized this, when he said,

Insofar as mathematics is true, it does not describe the real world. Insofar as it describes the real world, it is not true.

Yet the mathematical analogy is the safest, and the preferred analogy for physics. It is quite free of emotional baggage, and it is adaptable to any situation that might arise. To be fair, we must note its dangers.

Mathematical equations suggest or imply a false sense of precision and accuracy. The equation for a law or principle, presented without disclaimers and qualifications, fails to convey the limitations of scope and precision that apply.
Equations alone don't distinguish quantities that are directly measurable and observable, such as mass, length and time, and those that are useful invented concepts, such as energy, momentum, field strength, wave function, etc.
Students often fail to recognize "unphysical" consequences of an equation. Any of the equations for fields such as inverse square fields "blow up" to infinite values at r = 0. Any limit taken by calculus methods obviously can't be taken all the way to zero values of dx or dt at the quantum level.
Mathematical expressions of fields and wave functions tempt students to think of these things as having a "real" existence on a par with macroscopic quantities like mass or distance.

These misconceptions are not the fault of mathematics, nor the fault of physicists. Physicists are fully aware of these facts, and in a full treatment of theory they are all dealt with properly. It is only when the physics is diluted, simplified or dummied down for popular consumption, that important qualifications and disclaimers are left on the cutting-room floor.

The bottom line.

Do analogies permanently harm our students' understanding of physics? After all, physics is taught as a series of revelations: successive approximations supposedly getting closer and closer to the ever-elusive "truth." Better students cope with this quite nicely; they have what it takes to become physics majors. Others may learn just enough physics, mostly incorrect, to be dangerous if they actually tried to apply it. Fortunately they usually never have to apply it in a creative manner. They choose "procedure intensive" jobs where they blindly follow established practice without needing genuine understanding. This, I am convinced, is responsible for many technological mistakes, blunders and even disasters, is one reason for so much professional malpractice litigation, and for the high cost of liability and malpractice insurance.

Having observed many pre-medical and other pre-professional students who take our physics courses, and having experienced first hand many doctors who admit that physics was their "worst" and "most hated" course in college, I am convinced that if your life ever depended on your physician's knowledge of physics, you might as well say your prayers, it would do as much good. Fortunately most medical procedures, as practiced, do not require a physician to understand physics. Maybe I'd rather they not try, if I'm the guinea pig.

Fortunately for students, most jobs and professions that require a college diploma don't actually require a college education.

Appendix: How Exams Reinforce
Student Misconceptions and Bad Teaching.

One problem with educational research is that adequate double blind controls are not achievable in classroom "studies". In order to do such a study

Two groups of students would be selected to be fully statistically representative of the larger population of all students nationwide.
The two groups would be taught by different methodologies.
The testing instruments (exams) would be constructed by someone who did not know either group, or know either teacher and did not know what each one taught and how it was taught.
The testing instrument would be scored by someone who was also "blind" to the students, the teacher, the teaching methodology and the person who constructed the exam.

But there would still remain questions about whether the exam questions are representative of what should be learned in a physics course. Do they test merely information? Do they test creativity or effective thinking processes?

Has any piece of educational "research" ever met these standards?

Question for students: Do you understand all you know about it?

I have had many teachers tell me that their particular teaching methods are superior to others, the evidence being that their students do well on their exams. But who constructed the exams? Is it possible that the exams were unconsciously biased to favor the teaching methods and content of the course—all determined by the teacher? Could the exams have been selectively testing only those things the teacher emphasized, and evaluated by comparison with answers the teacher favored?

Even if the exams are supplied by an independent source, they likely reflect the community standards and biases of the physics education community. They usually include questions just like those posed in the textbook and by the teacher (and the assigned homework, if any). They conveniently neglect any questions that go beyond what could be mastered by a diligent student using only rote memorization.

For example, consider the picket fence polarization analogy discussed above. If it is "taught" in the course, simple exam questions can be posed that could be easily answered correctly using the analogy. But if a question were posed about three polarizers, the students would likely use the analogy and reach wrong conclusions. "This would be unfair," someone might object. "Students can't be expected to know what they have not been taught." Of course. But it illustrates the fact that the system of teaching and exams has the potential to teach, and reward, false information, misconceptions, bad physics, and even utter nonsense, then conclude that it has all been a great success, for the exam scores "prove" it. Are we collectively deceiving ourselves?

ENDNOTES

Descartes' derivation appears in his Dioptric, II. A good discussion of this may be found in Sabra, A. I. Theories of Light from Descartes to Newton. Oldbourne, 1967.
How many students have ever thought of this simple fact? How many teachers prod them to do so? To figure this out will strengthen the student's understanding of the reason for the inverse square law in 3-D, and will reveal its relation to conservation of energy. Students might also ponder the question of how this would work in a non-Euclidean universe, in which the area of a sphere is not proportional to the square of its radius. I recommend students read Abbott's Flatland and Dewdeney's Planiverse.
This web page has been in place some 20 years now, and no one has yet sent me an example of a "safe" analogy.

WORKS REFERENCED:

Abbott, Edwin [1838-1926]. Flatland, a romance of many dimensions. With illustrations by the author, A Square ... New and rev. ed. London, Seeley, 1884.

Dewdney, A. K. The planiverse, computer contact with a two-dimensional world. New York, Poseidon Press, c1984.

I'm always on the lookout for more examples, including examples of outright lies that textbooks tell. Send your favorites to me at the address shown to the right.

Return to Donald Simanek's

front page with the full menu,
education page,
physics page.