Things you can't MAKE.

The difficult we do right away. The impossible takes somewhat longer. —Engineer's joke.
MAKE readers enjoy making things, some of which are useful in innovative, or just plain weird, ways. Some work well and reach the pages of this magazine. Some great ideas just don't work out in the real world. Some ideas are just plain misguided.

For a change of pace, having recently neglected "teasers" in these pages, I put some thought to things you simply can't make, no matter how clever and ingenious you are. There are still folks who think that "anything is possible if you tinker with it enough". Let me demolish that naive notion.

Nature behaves according to fundamental laws. We can discover some of these and express them in our own language of mathematics, elevating them to the status of "laws" of nature. Newton's laws, conservation laws, and most importantly, the laws of geometry, describe how nature works. There's good reason to suppose that all laws of nature arise from the limitations of the geometry of the universe. When we have formulated and thoroughly tested a law about how nature works and are certain it doesn't contradict other known laws, that same law is telling us how nature doesn't work.

Another diabolical thing about nature is how inter-related its basic physics laws are. You can't violate one of them without violating many others. Nature blocks us from violating any one of its solid backbone of fundamental laws, those laws that are so well and thoroughly tested that they will likely survive any future advances in science. These will not cease working just because our knowledge of science advances.

Examples of futile projects.

Can you cut a triangle from a flat piece of paper that has exactly equal sides, but unequal angles? Silly idea, you say. That would violate laws of Euclidean geometry, and we know that our neighborhood of the universe obeys Euclidean geometry at least to the precision that we are capable of measuring.

Can you design a walking path that is downhill all the way around — in either direction, clockwise or counterclockwise? It's an old joke, "When I was a kid I had to walk two miles to and from school everyday, uphill both ways." We laugh because we know it is impossible. This says something about the laws of processes that operate around closed paths. Perpetual motion machine inventors ought to take this seriously.

Could you cut from wood a cube with seven faces? That violates the logical definition of cube. That's like making a four sided triangle. But a sphere with surface area of only 4 times the square of its radius is another class of impossibility, one that isn't merely a logical paradox, but a violation of a geometric property of the real world.

Try making a wooden box with hinged lid with a remarkable property. Put three genuine hen's eggs in the empty box, and close the lid. When you reopen the box you find four hen's eggs, which when broken, are found to be perfectly genuine. No gimmicks in the box, no sleight of hand. Good trick if you could do it, but nature doesn't work that way.

Apparent impossibilities.

Ever since craftsmen made wooden models of sailing ships inside of glass bottles, people have delighted in making "seemingly impossible" artifacts. The peach inside a glass bottle of peach brandy is one example. The neck of the bottle is far too small for a peach, but just right for the branch and pollinated blossom of a peach tree. Time in the summer sunshine does the rest. You can buy bottles with small necks with a complete pack of playing cards inside, still sealed with the tax label. The mystery of how it's done would be answered by watching someone painstakingly make one, but then the finished object would seem less fascinating. And of course there are the tiny bottles with a genuine coin inside, the bottle having been blown around the coin. See Impossible Bottle in The Wikipedia.

Visual illusions are usually two dimensional artistic depictions of things not possible in three dimensional space. Here's one of mine. I finished it in 2004, and have seen it reproduced without credit many places since. At casual glance it seems to depict two flat washers interlocked. But then you notice that the interlocking would be impossible if the washers were really flat. And even worse, each washer is self-contradictory in its depiction, taking advantage of the depth ambiguity of the near and far edges of ellipses. The colored faces and edges give the game away. The front faces seem to connect with back edges of each. Many illusion pictures, being rendered on a flat surface, succeed by such artistic ambiguities of perspective. The illusion would be destroyed if depicted from a different angle. Some clever artists make sculptures that appear to be entirely different things when seen from different angles, and the next step is sculptures that appear to be different illusions when seen from different angles.

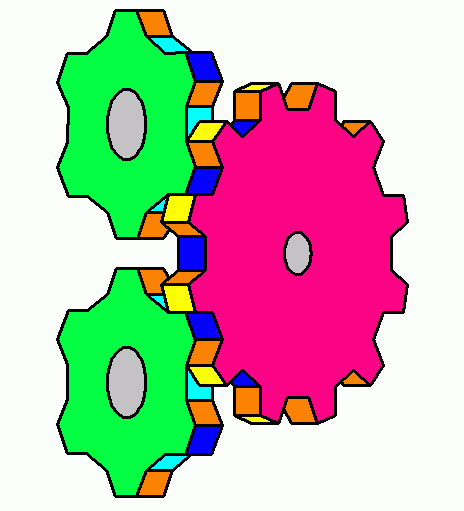
Gears are useful for those who make machinery. But pesky friction is ever-present. This inspired me to design the three-gear system above. As the gears mesh, gear teeth are transformed to a indeterminate quantum state where they are neither here nor there, and it is impossible to determine which gear they belong to. It is well known that there's no friction in quantum mechanics, so these gears must be perfectly efficient. At least that's my theory. I've colored the faces of the teeth to make it easier for you to understand the principle. I haven't built these yet; I leave that for others. I hoped someone more skilled than I might produce an animated version showing the gears rotating and the gear teeth morphing where they mesh.

Often the geometric peculiarities of isometric perspective is the trick that makes these illusion pictures perplexing. Isometric perspective removes the vanishing points of photographic perspective, so that parallel lines in the scene do not converge in the picture, but remain parallel. It is often used in engineering drawings. In such pictures there is no size reduction with distance so all dimensions may be measured with a ruler laid on the picture. So, could such an illusion be photographed? My experimental photograph of an impossible triangle made from Lego ™ blocks was achieved with a six inch diamter magnifying lens and an inexpensive digital camera at its focal point. The Lego™ model was just 7 inches in front of the magnifying lens. It takes some fussy tweaking to adjust the distances and alignment to renders reality in isometric perspective.

The "rear" column has two blocks, the "front" one has four, yet they are the same size blocks. Notice how the far edge of the green base plate seems larger than the near edge. Yet careful measurement of the picture, using a ruler, shows that it isn't. If this were "normal" classical photographic perspective the far edge would be shorter on the picture. You can make such pictures yourself. See Telecentric Lens Systems. Commercial telecentric system cost thousands of dollars, but this system demonstrates that the principle works for illusions. Even though this is far from "perfect" it required no post production manipulation with software. Can such pictures work in stereo 3d photography? I've not done it yet, but it may be possible by using some other deceptions. Can ordinary artistic illusions be rendered in 3d? Some can. For examples see my web page 3d illusions.

Digital photo taken with simple telecentric lens system.
Lego ™ blocks unaltered. No retouching was done.
Lens spherical aberration not corrected.

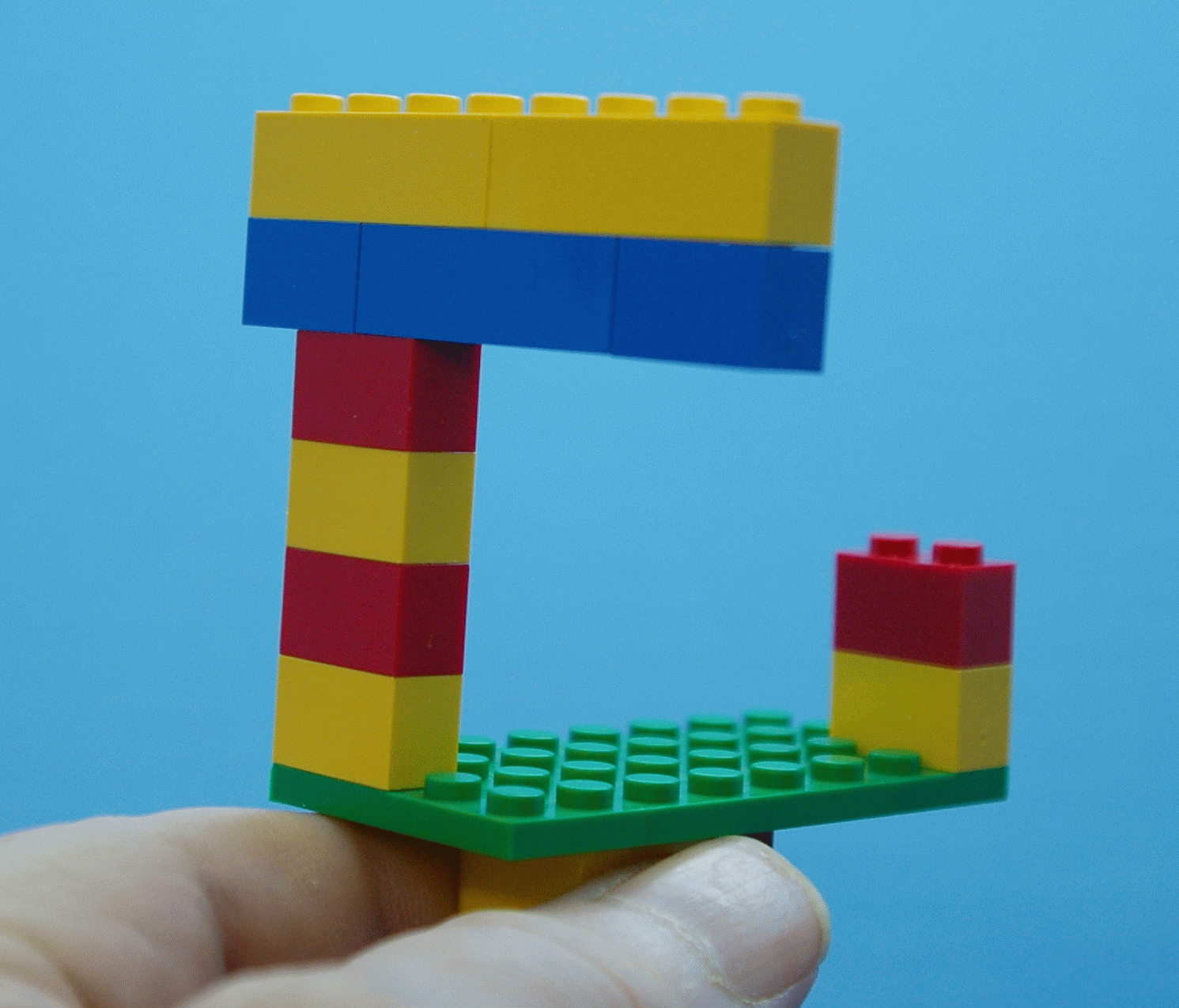Similar Lego ™ model taken with a normal lens.
Note convergence of parallal lines.

The web has examples of such illusion constructions, but these usually depend on doing surgery on the plastic blocks, or computer manipulation of the image. I assure you that no Lego ™ blocks were damaged or modified in creating my illusion photograph, and no retouching was done afterwards.

Gregory Hayes, photo editor at MAKE, was bitten by the challenge to make a Lego illusion photo without digital manipulations, and produced this excellent result. He tells me he did not use a telecentric system, and did not alter the lego parts. So how did he do it?

Lego Illusion photo by Gregory Hayes.

We mustn't forget that these illusions are only lines and colors on a flat page. It is our brain that, from long experience, conditions us to interpret them as if they were familiar objects like washers, gears and rectangular blocks.

We can imagine many things that nature doesn't allow us to make, we just don't always know in advance which these are. But sometimes nature has already told us all we need to know to conclude that they are impossible, and pursuing them would be futile, like finding the end of a rainbow. Some things that aren't possible in reality may be faked by various forms of deceptive illusion. And some things, like a three-sided flat coin that can be freely examined will take considerably longer to achieve. Like forever.

Exercise for the reader. Find a way to make a model of three real gears interlocked (each one meshing with both of the others) so that they all can freely turn. That's an easy one. Now try to make the gears turn on their own axles. See Whoops!

I've tossed out some challenges above. Send responses to dsimanek@lhup.edu to be added to an accessible web page on the subject make illusions.

Illusions and photographs are by Donald Simanek, except as noted.

[End of MAKE article. 1,344 words.]

The linked rings picture is larger than it appears on this page. It is also availaible in a version with five times the resolution. It is linked below, if you wish to use it on the cover.

The last paragraph "Exercise for the reader" may be omitted.

Larger versions of pictures.

Linked-C.jpg, 1088 x 1103 pixels. Probably not the best choice for clarity.

Linked-C.png, 1088 x 1103 pixels.

Linked-C.gif, 1088 x 1103 pixels.

Linked-C.pcx, 1088 x 1103 pixels. This PCX probably won't display in your browser, but you should be able to download it. PCX is a "no-compression, no-loss" format.

Lego illusion photo. 1221 x 1341 pixels.