Golden Star Origami
by Donald E. Simanek
 |
The star shown here is sometimes called the "golden star", widely used around the world in flags, heraldry, coats of arms and other decorations. It has been used in American flags of many designs from the earliest days of our republic.
Historical legend tells us that seamstress Betsy Ross was visited in 1776 by George Washington, Robert Morris and George Ross, who asked her to make an American flag conforming to a resolution of the Continental Congress. Washington's design had 13 alternating stripes of white and red, and thirteen 6 pointed stars on a field of blue. Betsy suggested five-pointed stars instead. When someone wondered whether five pointed stars would more difficult to make, Betsy showed how fabric could be cleverly folded to allow a five-pointed star to be made with just one cut of the scissors.
It's a pretty story, but like many fables of our early history, it's probably a myth. Contemporary documentation of it is totally lacking. Betsy's grandson first related the story in 1870, nearly a century after the fact, admitting that he had no confirmation other than stories passed down in the family. The story quickly proliferated, being published in Harper's Monthly in 1873, finding its way into other publications and even into textbooks, persisting even now. The Betsy Ross house in Philadelphia is the second most visited historic site there, but there's no hard evidence that Betsy ever lived there.
We'll leave historians to sort all that out. You can find out more about the flag myth at http://americanhistory.about.com/od/americana/a/american_flag.htm. What catches my interest is the method of folding cloth to allow the five pointed star to be obtained with a single scissors cut. This is the one believable detail in this story. Creating five-fold symmetric figures is a challenge in Euclidean geometry, and with paper folding, too. But a method is well known to quilters and seamstresses and was surely known to flag makers of colonial times and earlier.
 Here's how you can make a star template using a sheet of thin 8.5 x 10 inch paper. First cut off one inch from an 8.5 x 11 inch sheet.
Here's how you can make a star template using a sheet of thin 8.5 x 10 inch paper. First cut off one inch from an 8.5 x 11 inch sheet.
Fold the paper in half, to 8.5 x 5 inches, with the fold at the top.
Fold the paper to make a temporary crease to locate lines through the midpoints of the edges. These are shown dotted.
Mark the upper right corner "A" so you won't lose track of it. Mark the upper left corner "B".
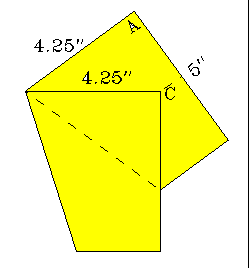 Bring corner B over to the horizontal crease. Be sure that it folds at the midpoint of the upper edge. Corner B does not go all the way to the right edge.
Bring corner B over to the horizontal crease. Be sure that it folds at the midpoint of the upper edge. Corner B does not go all the way to the right edge.
You have now created the angle that will be the foundation of the remaining construction. The angle is approximately 36.031879°. This is a bit larger than 360/10°, one tenth of a full circle, but very close to what we need to define the polygon vertices that are the basis of a five-pointed star. This is an approximate construction, not a strictly Euclidean construction. [Euclidian constructions don't use measuring tools. This construction starts with a measured rectangle of paper.]
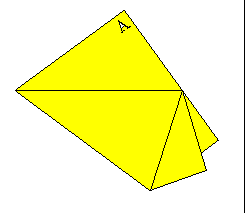 Fold the lower left edge up to lie along the slanted fold that passes through point C.
Fold the lower left edge up to lie along the slanted fold that passes through point C.
Fold the upper edge back so that all edges coincide and make the angle of approximately 36°.
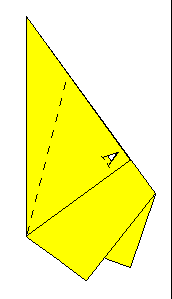 Now turn the whole thing over. Notice that there's a right triangle on the top of the folded stack of paper. You will now use suitably heavy scissors to cut the whole stack along the dotted line. The line starts at the lower left vertex of the triangle and ends on the fold of the triangle's opposite side at a point measured 1/3 of the length of that opposite side from the triangle's upper vertex.
Now turn the whole thing over. Notice that there's a right triangle on the top of the folded stack of paper. You will now use suitably heavy scissors to cut the whole stack along the dotted line. The line starts at the lower left vertex of the triangle and ends on the fold of the triangle's opposite side at a point measured 1/3 of the length of that opposite side from the triangle's upper vertex.
You should now have a near-perfect five-pointed star like the one shown above. Other variations can be obtained by tilting the cut line differently. Cut from the lower corner to the midpoint of the opposite side and you get a "fat" star. Experiment for other variations.
The remainder of the sheet of paper can be used as a painter's mask to decorate your house or automobile with painted stars.
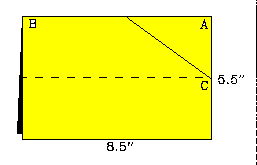 One wonders whether 8.5 x 10 inch paper was common in 1776. Today the standard is 8.5 x 11 inch paper. One can make the star beginning with this modern size quite easily. Only the first two steps are different. Fold the sheet in half with the fold at the top. Now locate the midpont of the 5-inch edge, and bring the opposite top corner (B) down to that point (C) on the right edge. This forms the starting angle, which is 35.85584°. This is smaller than 36°, but the resulting star is still quite good, for each of the many folds and the thickness of the paper adds a bit to the angles. The remaining steps are the same.
One wonders whether 8.5 x 10 inch paper was common in 1776. Today the standard is 8.5 x 11 inch paper. One can make the star beginning with this modern size quite easily. Only the first two steps are different. Fold the sheet in half with the fold at the top. Now locate the midpont of the 5-inch edge, and bring the opposite top corner (B) down to that point (C) on the right edge. This forms the starting angle, which is 35.85584°. This is smaller than 36°, but the resulting star is still quite good, for each of the many folds and the thickness of the paper adds a bit to the angles. The remaining steps are the same.
Paper of size 8.5 x 11 inches goes back to Europe in 1600, the result of a 17 x 22 inch sheet cut into four pieces. At about the time of the first World War this size became a standard for business purposes in the USA (the government and military standard paper was smaller).
I shall resist idle speculation about how the size of paper necessary for this construction might mystically relate to the Golden Mean or to the Fibonacci sequence.
 |
Congress did not specify how the stars were to be arranged. Many flags of that time and earlier had "stars and stripes", with the stars arranged in various ways. Flags with stars in a circle were rare. A painting by Charles H. Weisgerber, made in 1870, showed Betsy Ross stitching a flag with stars in a circle while George Washington and two other members of the committee look on. That suggests another mystery. What trick of geometry, or origami, would you need in order to arrange 13 stars perfectly spaced around a circle?