Cannonball collision.

One 12-pounder mountain cannon is located on the top of a cliff, 200 yards elevated above the flat battlefield. Some 500 yards away on the battlefield below is another similar cannon. The battlefield is uninhabited. Normally in these re-enactments actual cannonballs aren't used, but they just happen to have a few 9 lb cannonballs handy.

Joe suggests, "Let's see whether we can aim the cannons so that two cannonballs collide in mid-air. We could aim these two cannons toward each other so the cannonballs collide somewhere between. Of course we'll have to be lucky to aim that accurately, but we might come close."

Moe agrees to go along with this. "But how should we aim the cannons so we don't hit each other?"

"Easy. Just aim each cannon directly toward the other cannon. Since the cannonball trajectories curve downward neither one can possibly hit the other cannon. Aimed that way the paths of the balls are certain to pass very close to each other at least."

Moe is still skeptical. "How can you know that? These cannons aren't identical, and the charge of gunpowder may not be the same in each."

"Doesn't matter," Joe said confidently. "If the cannons are fired at the same time the cannonballs will both reach the crossing point of their trajectories at the same time, even if they have different weights and even if their initial velocities are different."

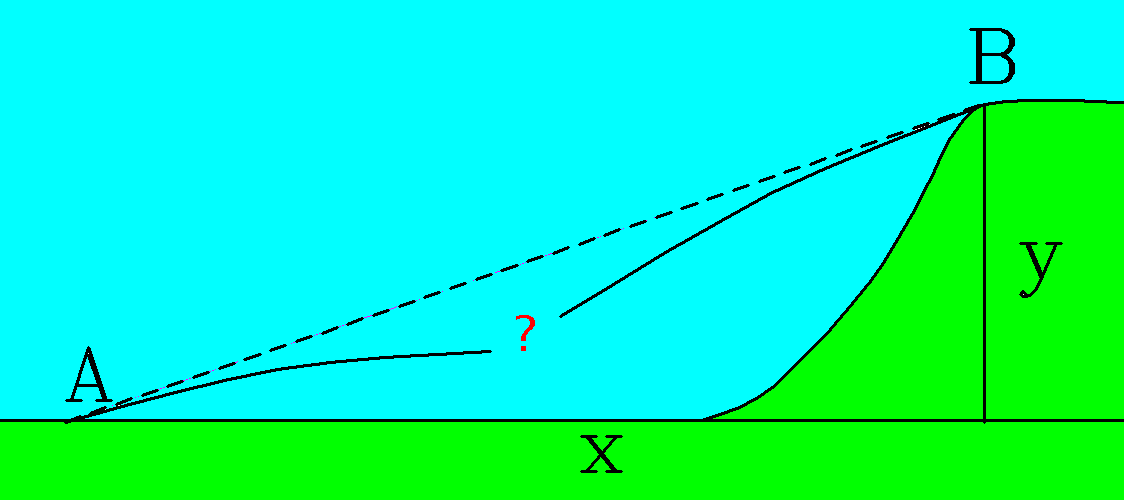Fig. 1. Cannons at A and B aimed directly toward each other along dotted line AB. Cannon B is elevated y = 200 yards. The cannons are separated by x = 500 yards.

How does Joe know all these things without complicated calculations?

Answer.

The two influences are the gunpowder that gives the cannonball its initial velocity, and gravitational force that causes it to fall downward. If there were no gravity, the cannon balls headed directly toward each other would travel along the same straight line AB and would be certain to collide somewhere along that line, call it point P. We don't need to calculate where point P is located. Now if we "turn on" gravity, it causes each ball to fall according to y = ½gt² where y is the distance of fall, g is the acceleration due to gravity and t is the time of fall. Both cannon balls have traveled for the same time, so during that time they would drop the same distance from point P, which guarantees collision.

A small difference in firing times won't matter. That will only shift the crossing point of the trajectories.

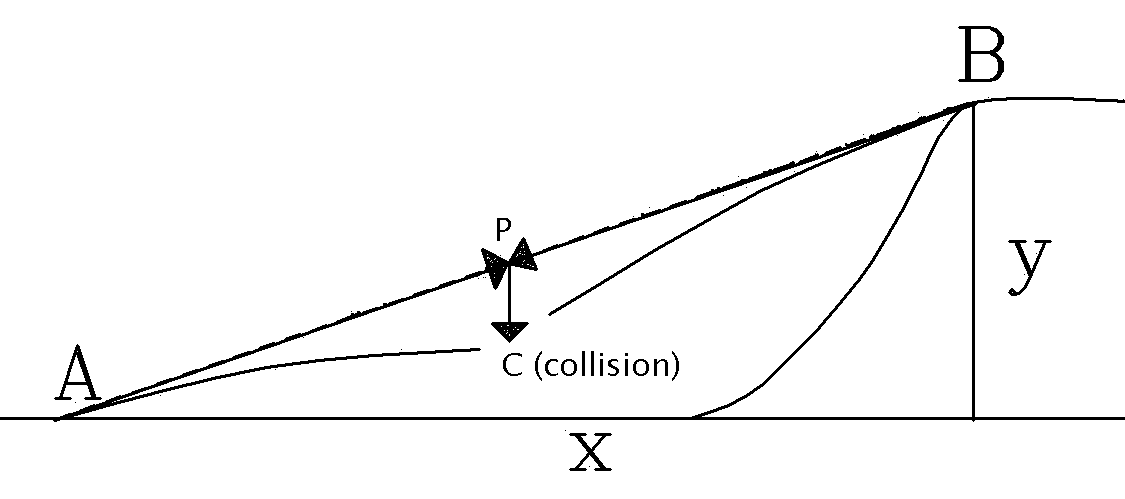Fig 2. The collision is inevitable.

For those who like a vector approach, this diagram shows the vector AP of length v_at, the vector BP of length v_bt, and the vector PC of length ½gt², which is the same for both cannonballs. Clearly the initial velocities v_a and v_b need not be equal. The resultant vectors AC and BC (not shown) are the vector displacements of the cannonballs during their trajectories, given by equations of the form d = v_ot + ½gt².

Reader feedback is appreciated. Email dsimanek@lhup.edu. If you have a favorite physics puzzle that is not well known, not easily found on the web, or in the many published physics problem books, send it along. Include your answer, if you have one. If your idea is used, we'll credit you. I especially like puzzles that can be solved with insightful and simple arguments, preferably with minimal mathematics.