Weighing moving masses.

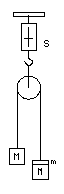
The Atwood machine shown is suspended from a spring balance. The mass on one hanger is M, that on the other is (M+m). Suppose the heavier side (right side) hanger is fastened to the top pulley by a thread. The spring scale, s, reads (2M+m). The restraining thread is burned (or cut) and the system accelerates. During the motion of the masses the spring balance reads

1. the same as before.
2. more than before.
3. less than before.
4. zero.

Answer.

As the masses move, their center of mass moves (actually accelerates) downward. You can demonstrate the effect of that by standing on a bathroom scale, and then suddenly bend your knees to lower your own center of mass. In this case the scale will register a smaller value during this acceleration, and as you quickly stand up straight again, it will register a larger value than your static weight.

This problem has a lot of physics. Ernst Mach spends many pages on this in his 1893 book The Science of Mechanics.

When the masses are at rest, the spring scale reads a force of (2M+m)g, which is the tension in the supporting string. But when the masses are accelerating, their center of mass accelerates downward, you might think the scale reading would be larger. So the result is a bit counter-intuitive. I like problems like that.

Brute force mathematical derivation isn't necessary to obtain an intuitive answer to the question.

The scale exerts an upward force F_scale = (2M+m)a where a is the downward acceleration of the center of mass.

If the masses weren't accelerating, the spring balance would exert a force of just (2M+m)g, the total weight of the suspended masses. When they are accelerating, M moving up, and (M+m) moving down at the same instantaneous speed, the center of mass of the two amounts M remains fixed. But the center of mass of the small additional mass m moves downward with acceleration a. The spring scale reading is therefore reduced by amount ΔF = m(g-a).

In the above derivations I took the unorthodox strategy of labeling the masses on the atwood machine as M and (M+m). This expresses results in terms of the unbalance amount, m. Here's an example of where that strategy pays off. Let's find the force, S registered by the spring balance without finding the tension in the string, by looking at what happens to the center of mass of the system.

The center of mass of the two masses of size M does not move. The unbalanced extra mass m accelerates downward at value a. So the spring balance reading, S, is an amount ma less than in the static case, ie.

S = (2M+m)g - ma

This reduces to

S = 4M(M+m)g/(2M+m) .

A related, but distinctly different (no contradiction here) phenomena is demonstrated by putting a running motor on a platform scale. The scale may read more or less when the motor is running than when it isn't. How can this be?