Finding Equilibrium.
Textbook problems about mechanical systems often look as if desisgned by Rube Goldberg, and seem to have no possible application. But this one is inspired by a patented system that does have practical uses. Its mechanical principle is found in commercial products you have likely used. It once given as a college physics problem assignment, leading to development of a very important precision scientific instrument. I'll say no more now, to avoid giving away the solution.
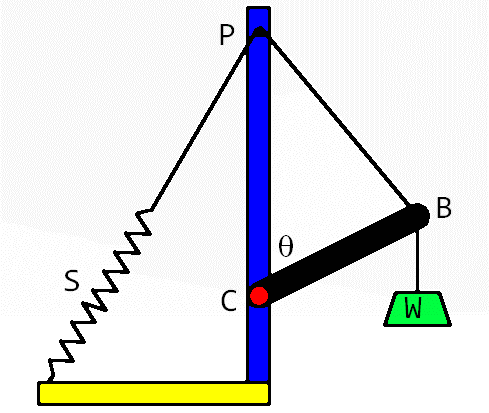 |
| Where does this system balance?. |
|---|
A rigid arm CB freely pivots at frictionless axle C, and has a weight W at its other end, B. A string at B passes over the small, frictionless peg P and then to one end of a spring, S. The other end of the spring is firmly attached to the solid base plate. The rigid arm is shown at angle θ but it can freely rotate about frictionless axle C over a range from 0° to 180°.
The peg at P is so small that its size may be neglected in the analysis. Assume its friction is negligible. To make this interesting, the relation between spring constant and weight is chosen to be k = W/a, where a is the length CP.
If the weight W is allowed to move freely, is there any position of the arm CB where the system is in static equilibrium? If so, find it.
Answer.
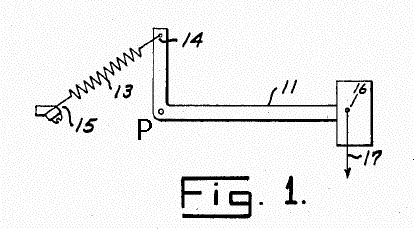 |
| One of LaCoste's mechanisms from US patent 2,293,437. |
|---|
The system is in equilibrium for any angle of θ from 0° to 180°. This puzzle is a modified form of an equipoise system patented in 1942 by Lücien La Coste and Arnold Romberg (US 2,293,437). Their patent makes use of a "zero length spring", a spring that is wound under tension so that its force law is kL, where L is the length of the stretched spring. Ordinary springs obey Hooke's law kx, where x is the amount of stretch measured from the unloaded condition. Zero length springs are now found in articulated arm desk lamps, garage door systems, and any application that requres a system to be in equilibrium over a range of angles. Such systems are called equipoise mechanisms.
 |
| An anglepoise lamp with four zero-length springs. The system is in equilibrium at all positions of the arms and the lamp head maintains constant angle in all positions. |
|---|
The idea grew out of a problem posed by Romberg to LaCoste, in a class at the University of Texas, asking for an improved design for a vertical pendulum seismograph as good as the existing horizontal pendulum instruments. LaCoste brainstormed this for a couple of weeks, finally arriving at a system using a zero-length spring. Romberg suggested ways that such springs could be constructed. This collaboration led to a published paper, later to patents and finally to a successful partnership for construction and sales of sensitive gravimeters. The necessary requirement for these is to cause a mass acting as a pendulum to have a very long (ideally infinite) period of oscillation, but contained in a small, lightweight package.
The idea had been previously patented by George Carwardine in 1932, as part of an "anglepoise" lamp design. Zero length springs were apparently invented even earlier, but were not well known then.
Our puzzle avoided the use of a zero length spring, by using an ordinary spring and a frictionless peg to provide a fixed pivot point for the string segment CB, so that segment acts as if it were a zero length spring. But because of inevitable friction at the peg, it is impractical for a sensitive seismograph or gravimeter. The mathematics is straightforward, but the result is surprising.
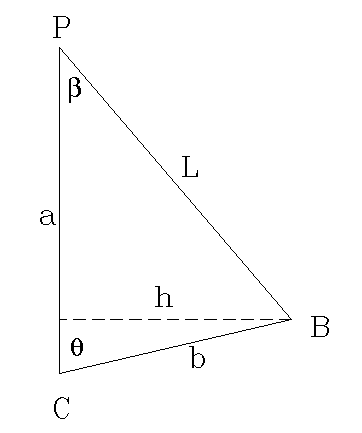 |
| The geometry of the device. |
|---|
Let the distance CP = a and the distance CB = b. Consider torques about the pivot point C. The torque due to the weight W is
τg = W b sinθ.
The length PB is L. Draw a line h from C, perpendicular to PB. It's length is:
h = a sinβ.
From the law of sines,
L = b sinθ/sinβ.
The torque due to the spring is τs = - k L h.
τs = - k (b sinθ/sinβ) a sinβ.
The net torque is
τg + τs = W b sinθ - k a b sinθ = (W b - k a b) sinθ.
If W = k a then the torque on bar CB is zero for any angle, θ, the system is in equilibrium at any angle from 0° to 180°. The length, b, of the bar doesn't matter either, so long as it satisfies the requirements of a triangle.
This condition is satisfied by our assertion that the relation between spring constant and weight is k = W/a.
References.
Lucien LaCoste from the Wikipedia.Lucien J. B. LaCoste: Portrait of a Scientist–Inventor.
History documents from the University of Texas.
Web searches for "equipoise" are futile, for the word has been usurped by promoters of medical products. You will get more interesting hits by searching for "zero length springs".
Return to Physics puzzles.
Return to the Donald Simanek's home page.