Archimedes' Hat Box Theorem.

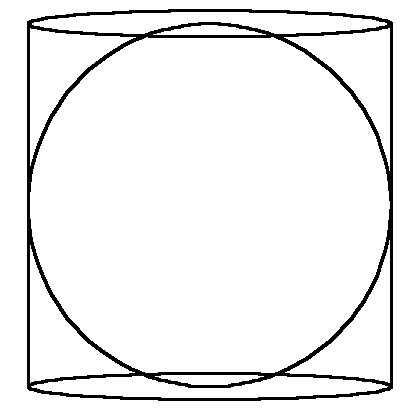Archimedes' hatbox.

Archimedes of Syracuse (c. 287 - c. 212) was a master of geometry, using clever methods and Euclidean geometry to establish results that much later in history would yeild to the methods of integral calculus. Some of his writings have been lost, but we have enough of them to see that he often blurred the boundaries between physics and mathematics in order to achieve remarkable results.

While puzzling how to find the surface area of a sphere, he discovered a result that has since been named "Archimedes' hat box theorem" because of the figure that describes it. It says: "The area of a sphere of radius R is equal to the area of a cylinder of radius R and height 2R."

This is an astoundingly simple result, that would not have been at all obvious to most people. It is a standard exercise in calculus courses today. But how can it be shown without using calculus, without even knowing the formula L = 2πR for the circumference of a circle, and without using π in any way?

Answer.

Archimedes' Hat Box solution.

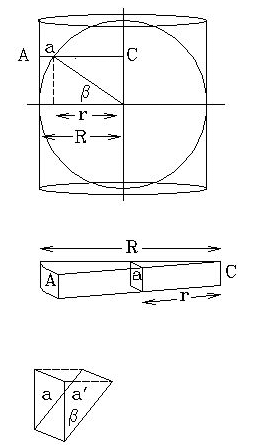
The first figure shows the sphere inside the cylinder. Both have radius R. Consider a very tiny patch of area A on the cylinder, perhaps "rectangular" in shape. Draw radial lines from its corners to the vertical axis, forming a pie-shaped narrow wedge.

Where this intersects the sphere at distance r from the axis a smaller rectangle, a, may be imagined. For now let it be formed with two sides parallel to the vertical axis ands the other sides (actually arcs) in a horizontal plane. It is smaller than A, of size a = Acosβ.

Now we must tilt area a through angle β. We use the fact that a/A = r/R. This projects A onto the sphere, as area a' = a/cosβ = Acosβ /cosβ = A.

Now, this is true for any tiny area A projected onto the sphere, so if all such areas are summed, we conclude that the area of the sphere equals the area of the cylinder.

Of course, Archimedes didn't have our modern methods of algebra or trigonometry. But the argument goes the same way if we use ratios of sides of similar triangles in the figure.