Physics puzzles.

Physics questions fall into several categories.

Questions about physical phenomena, dependent on real world data.
Questions that require theory and mathematics. Textbook end-of-chapter problems are usually of this sort. Sometimes these have idealized assumptions.
Questions that require sneaky, devious, clever, or insightful approaches. These are more properly called "puzzles".

When we look at the history of the sciences we find that many advances originated as puzzles, often solved by an untidy process of brainstorming, and sometimes, dumb luck. After finding an answer, the published papers are polished, sanitized and presented in "proper" academic language and style, often concealing the thought processes that actually led to the results. These end up in textbooks to serve as seemingly unattainable models for students. The thrill of the game is gone.

It was not always so. Books and published papers of 17th and 18th century science pioneers often recounted the creative process in detail, with all its false starts, dead ends, and failed hypotheses. Nowadays that is not considered proper style.

There are physics problems and physics puzzles. I like the puzzles. This collection encourages one to seek simple, clever and insightful methods to arrive at the answer. I especially like those that yield to only elementary mathematics. Some can also be solved by tedious formal mathematical analysis, but only as a last resort.

A few of these puzzles are quite old, with obscure sources. Some are my own invention. I have tried not to include puzzles whose correct answers can easily be found on the internet.

Themes.

Several categories of puzzles.

Define that! Puzzles that require one to use careful and precise defintions, or are stated with ambiguous definitions.
Self referential. Puzzles that have simple or conceptual answers only possible because of the special way in the puzzle was posed.
Trick puzzles. Puzzles that describe special situations that are (a) unphysical, or (b) have special conditions that allow simple resolution of an otherwise messy and difficult situation.
Conceptual confusions. Puzzles that exploit common misconceptions about nature, physics or mathematics.
Paradoxes (apparent). Puzzles posed to descrbe apparently contradictory or paradoxical situations or explanations.
Visual deceptions. Puzzles in which the accompanying diagram misleads or deceives. (Pictures can lie.)
Isn't that the limit? Puzzles that require great care in taking limits to zero and infinity. Many classic math paradox proofs (sometimes called "poofs") depend on this kind of deception, such as hidden division by zero. Like the proof that 2 + 2 = 5. (Well, it does, for sufficently large values of 2.)

For those who want answers, my answers can be found here: Puzzle Answers. They come with no guarantees, however.

Puzzles.

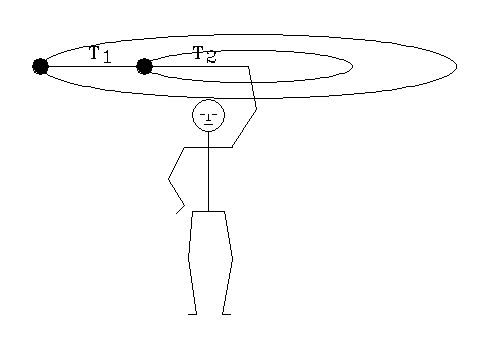
Going around in centripetal circles. Two identical masses (black) are connected by cords T₁ and T₂ of equal length, and swung around a "fixed" axis. If T₁ is given, what is T₂? Explain your answer without using the word "centrifugal". First make a quick guess. Then solve it correctly.
Nit-pickers may note that, due to gravity, this motion won't lie in a single plane, for the balls will orbit lower than the swinger's hand. Ignore this distraction.
The water bridge. In Europe there are a few unusual bridges. Normally the bridges (with a street or railroad on top) cross a river. But there are exceptions. Sometimes a canal is guided over the bridge that spans over a highway, or even over a river. These are called water bridges.

The Magdeburg Water Bridge. Photo from Sandra Sandrok Douglas.
Bridge designers take into account the maximum weight of traffic a bridge can support. How does that apply to water bridges? Assume that the level of water on such a bridge remains nearly constant as ships cross it, and so does the mass of water above the bridge—it might be 10,000 tons. A ship that travels the canal has a weight of 1000 tons. What is the extra load on the bridge when the ship is in the middle of the bridge?
The Magdeburg Water Bridge is a navigable aqueduct in Germany that connects the Elbe-Havel Canal to the Mittelland Canal, allowing ships to cross over the Elbe River. At 918 meters, it is the longest navigable aqueduct in the world.
Water bridges are rare in the USA. Stanton de Riel informs me of one.

The D&R Canal (Delaware and Raritan) has what you might consider a water bridge, over a tributary of the Millstone River, just north of Princeton, NJ. The canal is navigable, if currently only by canoe (commercial shipping having halted some time ago; the locks are not maintained any more).

Puzzle submitted by Hans-Peter Gramatke.
The Mighty Muscus. A fast train travels at 100 mph. A fly on collision course travels at 5 mph exactly opposing the train. The fly hits the window pane of the locomotive, gets stuck (RIP), and continues to move with the train—of course at 100 mph, the speed of the train. As the fly reversed its direction of movement, there must have been a point where it had a speed of zero, just for an instant. If the fly had the speed of zero, then just for that instant the train's speed must have also been zero. Explain how this strong fly could stop (even for a short instant) a train travelling at 100 mph.
Puzzle submitted by Hans-Peter Gramatke.
Drag race. Dick and Jane are doing a lab experiment, measuring friction by timing wooden blocks sliding down an inclined plane at constant speeds. The blocks measure 3 x 4 x 5 inches. Dick suggests a race, and predicts that if a block is sliding on its 3x4 face it will have smaller contact area and smaller friction than if the block is sliding on its 4x5 inch face, so with smaller frictional drag it will win the race when both slide down the plane. Jane disagrees, arguing that they still weigh the same, so the race will end in a tie. Who is right, and why?

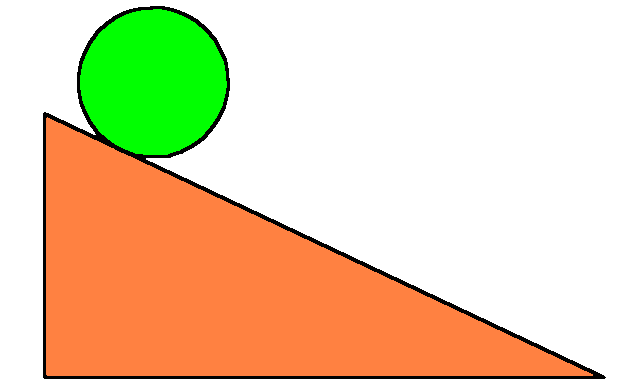
Rolling down an incline.
Off to the races. A standard physics problem (and demo) races cylinders rolling down an inclined plane. The cylinders are constructed to have the same mass and the same outer radius, but one is solid wood and the other is a metal hoop. The hoop, having the greater moment of inertia, accelerates less under the gravitational force, and loses the race.
But what if we handicap this race differently. Make two solid cylinders of the same length and radius, but of materials of very different density. They will have very unequal masses. Now which one will win, and why?
Now race two spherical balls of the same radius but different masses, say one of steel, one of wood. Which will win?
As usual in these puzzles, you may assume ideal materials, negligible friction and rolling without slipping (in spite of the absence of friction!). These puzzles may be resolved without explicit use of mathematics. Galileo could have solved them. Perhaps Archimedes could have.

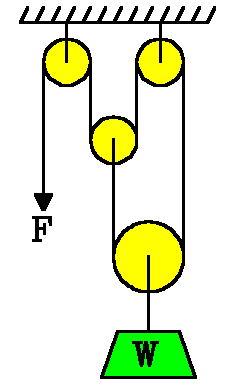
The confounded tackle.
The confounded tackle.. Every so often ingenious tinkerers try to improve on Archimedes. Here's a clever variation on standard pulley systems. Calculate its mechanical advantage, assuming frictionless, massless pulleys and perfectly flexible rope of negligible mass.
Soap Box Derby. A kid is building an unpowered downhill racing car. He has the brilliant idea of using, instead of four wheels, only three wheels, to reduce the friction on the car. Will this modification increase the car's performance in a downhill race? Why?
A very fair race. Some years ago someone had the bright idea to hold a hovercraft race. Hovercraft are supported above the ground by a large fan that forces air downward. The craft moves as if it were on a very low friction surface. These vehicles also have another fan for propulsion. They are rather large vehicles, so the race promoters designed a circular track that was banked so that vehicles at the inside of the track wouldn't have an advantage. Apparently the racetrack was never built, and no such races were ever run. Why?

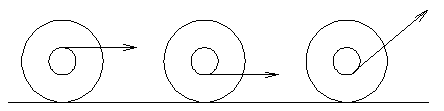
Pulling a yo-yo.
Yo-yo. A yo-yo toy rests on its edge on a level table.
1. If the string comes out above the axle, what will happen when you pull the string parallel to the table? Will it roll left, or right?
2. If the string comes out below the axle, what will happen when you pull the string parallel to the table?
3. If the string is pulled straight up, which way will it roll?
4. At what angle can you pull the string to cause it to slide along the table without rolling? The coefficient of sliding friction at the interface with the table is 0.5.
  Support your answers with analysis of fores.
Impact. Two identical round pucks rest on a frictionless level table. One puck is propelled toward a stationary puck. They collide, and the collision is perfectly elastic. Niether puck rotates before or after the collision. Prove that after collision, the velocities of the two pucks are at right angles, no matter how the collision occurred.
Levitation. Why doesn't this happen?

Morning levitation.
Burning the candle at both ends.

Harpo Marx burns the candle at both ends.
Horse Feathers (1932).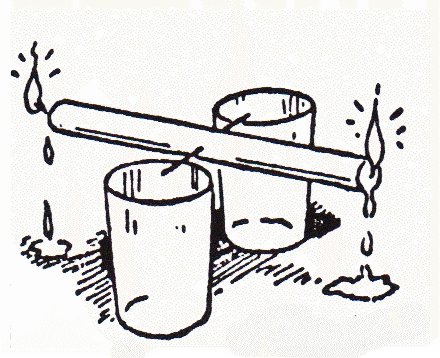

A candle is trimmed at the bottom so that both ends of the wick are exposed. A nail or long needle is pushed through the middle of the candle, and is supported on the rims of two glasses. The candle is then lit at both ends. Typically the candle will oscillate around the axle. Is the resulting motion simple harmonic motion or just periodic? Is its period constant?
Pressure Paradox. An old-fashioned bottle of nonhomogenized milk is left undisturbed. The cream in the milk rises to occupy the narrow neck at the narrower top of the bottle. Is the pressure of the milk on the bottom of the bottle now the same, greater, or less than before?
You know this puzzle is old, for those milk bottles are seldom seen today. Nor is unhomogenized milk common. However, many food products come in similar narrow-necked bottles. For a modern version imagine such a bottle of oil-and-vinegar salad dressing, shaken up. Then the oil slowly separates and rises to the narrow neck of the bottle. Note: Many materials, when mixed, occupy a volume different than their total volume when separate. This is generally a small effect. In this problem, this volume difference will be ignored. It would, in fact, have negligible contribution to the changes of pressure being considered here.
A pendulum has a bucket for the bob. It is half-filled with water. The water freezes. What happens to the period of the pendulum?
Thermal pressure. A solid cube rests on a level surface. The cube is heated by a large amount. Does the pressure the cube exerts on the surface,
1. increase?
2. remain the same?
3. decrease?
Disregard relativistic effects and stick to classial physics. Explain your reasoning.
A large ship moored at the dock has a rope ladder hanging over its side all the way into the water. Its steps are 30 cm apart, and 20 steps are above the water. The tide comes in at the rate of 15 cm/hour. After 6 hours how many steps are above water?
Stubborn Ball.

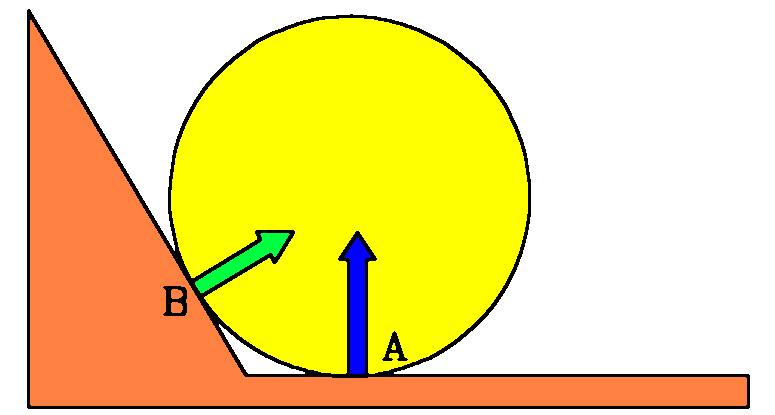
A smooth ball rests at the junction of the floor and a tilted wall. When bodies are in contact, there's a force at the interface, directed along the normal to the contact surface. We show the force due to the tilted wall (green) at B and the force due to the floor (blue) at A. The blue vector has no horizontal component, so it doesn't cause rolling of the ball. But the green vector does have a horizontal component. Why doesn't that force cause the ball to roll away from the wall?
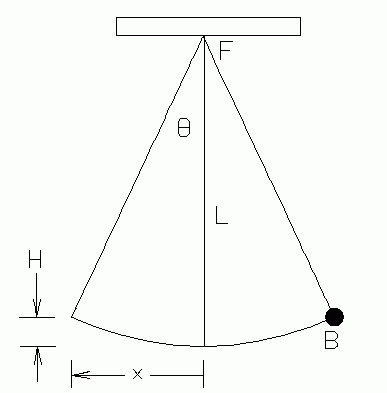
A simple pendulum has a small mass (B) attached to a string of negligible mass suspended from a fixed support (F). The tension of the string is not constant during the swing. For a pendulum with string length of L = 30 cm swinging in an arc of θ = 10° on either side of the vertical, how much work is done by the force of the string tension acting on the mass during one period of the pendudlum?
Rigid bodies. Newton's laws are said to be universal, that is they apply everywhere and at all times, at least for macroscopic (large scale) phenomena. Nearly every mechanics textbook has a chapter dealing with rigid bodies. Those are bodies that maintain their physical shape exactly during interactions. Show that perfectly rigid bodies cannot exist, for they would violate Newton's laws.
Weighty matters. Textbooks often define the weight of a body as the force that gravity exerts on a body at the earth's surface. But later on, they speak of situations where a body is fully or partially immersed in a liquid, and speak of "the loss of weight" of a body immersed in liquid. Then when discussing orbiting manned earth satellites they speak of "weightless astronauts". It is said that physics is a "precise" science, but it seems the language used in textbooks is far from precise. Resolve this dilemma.
Leonardo's goof 1. Leonardo da Vinci's notebooks have a number of errors.

Source: Leonardo da Vinci, Codex Arundel, folio 1030, drawing no. 68: London, British Museum
This drawing shows his military tank, powered, as shown at the left, by gears and cranks. Two people inside turned the cranks that drove the wheels. The gearing is the common "lantern gear" of the time. Ignoring the trivial observation that it would take two very strong men to power this, why wouldn't this work? There's no record that it was ever built and used.
Lenardo's goof 2. Lenardo da Vinci's notebooks have a number of errors. Here's one showing water streams from holes at various heights in a water tank.
What's wrong with this diagram. How should it look?

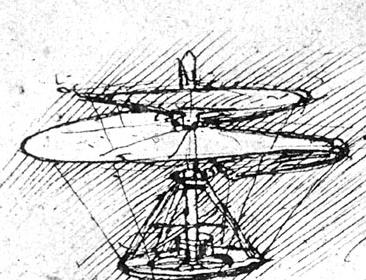
Leonardo's aerial screw. Codex Atlanticus.
Leonardo's goof 3. Leonardo da Vinci proposed several ideas for man-powered flying machines. One, called the "aerial screw", had a rotating screw-shaped airfoil, powered by two men on the platform below, turning cranks. Aside from the trivial observation that even two men wouldn't provide enough power, this idea has a serious flaw of physics that would prevent it from staying aloft. What is it? Obviously this idea didn't fly.
Textbooks often say that when an object is at the focal plane of a converging lens, the light from it, passing through the lens, forms a real image "at infinity". However it can equally well be said that it also forms a virtual image "at minus infinity", easily seen by looking through the lens toward the light source. So a single lens is producing two images. How can this be?
Are we playing fast and loose with the word "infinity" here? In some mathematics courses teachers used to say "parallel lines meet at infinity". More careless language, it seems. Resolve this confusion.
This raises another question. Any lens can produce real images or virtual images, depending on the location of the object, and given by the lens equation 1/p + 1/q = 1/f. But is this all? Does a lens produce any other images?
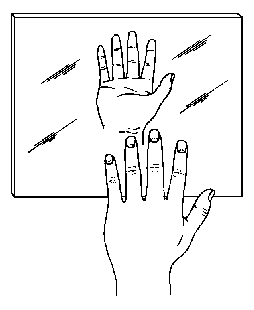
The image you see when you look in a mirror appears reversed left/right, but not up/down. If you are right handed, your mirror image is left handed. If you touch your right ear, your image touches its left ear. But your image is not standing on its head. At first this seems paradoxical for the mirror is symmetric about its normal. You can rotate the mirror around its normal axis, and the image does not rotate. So why isn't the image also symmetrical about this normal? Resolve this confusion with a simple argument. You must be careful and precise in your use of language.
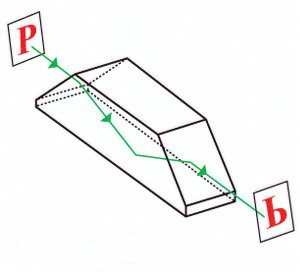
Virtual image rotation. A Dove prism has the interesting property that when you look through it and rotate it, the image rotates through an angle twice as large as the prism was rotated. Explain.
If you don't have such a prism, use an equilateral prism, looking through it, as shown, so that the light has internal reflection at one side of the prism.
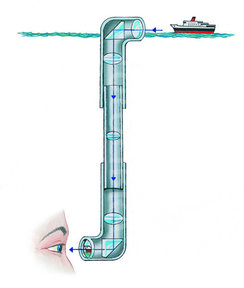
Up periscope. Submarines played an important role in WWII. You have seen those movies where the captain looks for enemy ships through a periscope, a long narrow tube extending upward to just above the water surface. Those were days before TV and fiber optics, so the periscope used only lenses and reflecting prisms. You know that looking through a long, narrow tube you cannot see more than a very narrow field of view, yet periscopes could see a much larger field. These periscopes could be 30 feet long and six inches in diameter. Looking through such a tube you'd see a field of only one degree. Yet perisocpes typically had fields of 9° or more. How can this be done using only an optical system with glass lenses?
The physics of falling. Every introductory physics textbook tells you that in the absence of air drag, two bodies of different mass fall with the same acceleration, that is, they will fall equal distances in equal times. Galileo is usually mentioned in this context, though others did the experiment before him, and he probably never did the experiment with freely falling bodies (certainly not at the leaning tower of Pisa). But Galileo had a simple logical argument to conclude that the mass of the falling body does not matter. Remember that in Galileo's time algebra had not been invented, and calculus came along even later. The concept of gravity and Newton's law F = ma also came later. So how did Galileo conclude this important result, using only a simple logical argument?

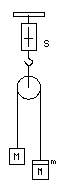
Weighing a
moving system.
Weight reduction? We are often told that if we keep moving we'll lose weight. But does a moving object's weight depend on its motion? A classic physics laboratory experiment is an Atwood machine: two unequal masses on the end of a string passing over a pulley. The system can be made to accelerate slowly enough to easily measure its acceleation, and with a little mahematics, determine value of the acceleration due to gravity. The Atwood machine shown is suspended from a spring balance. The mass on one hanger is M, that on the other is (M+m). Suppose the heavier side (right side) hanger is fastened to the hook of the spring balance by an additional thread, preventing the masses from moving. The scale reads (2M+m).
The restraining thread is burned or cut and the system is set in motion, the left side rising and the heavier right side falling. While the masses are in motion the spring balance reads
1. the same as before.
2. more than before.
3. less than before.
4. zero.
Explain why.
When discussing kinetic theory, textbooks often model an ideal gas as a box with infinitely massive walls containing very tiny particles bouncing from the walls. Part of the argument considers one such particle bouncing from the wall. We are told that the collision is perfectly elastic and the particle rebounds from the wall with the same speed it had before hitting the wall. That tells us that the ball rebounds with unchanged kinetic energy, which students are all too willing to accept uncritically. We reasonably conclude that no energy was lost to the wall. But what about momentum? The particle had momentum mv before the collsion, and momentum −mv after, since momentum is a vector. So there's a −2mv change in the particle's momentum, and from conservation of momentum, there must have been a change of +2mv change in the momentum of the wall.
So how can the wall gain momentum without gaining any energy? Are textbooks deceiving us again? Resolve this with an energy and momentum calculation.
Elastic definitions. Textbooks tell us that a perfectly elastic body is one which, when deformed, returns to its original shape without loss of energy. They also tell us that a perfectly elastic collision is one in which the participating bodies conserve both kinetic energy and momentum.

But consider a bell, made of brass with a brass clapper. Bells and their clappers are made of nearly elastic metals, and both preserve their shape after many collisions. A perfectlhy elastic collision is one that conserves mechanical energy without loss to dissipative processes. The collision of clapper and bell is not a perfectly elastic collision, for considerable energy is lost as sound, radiated away from the bell. Also the swinging bell and clapper soon come to rest, so you know their energy was dissipated somehow. So how can elastic bodies undergo inelastic collisions? Resolve this apparent contradiction.
Idle question: Would a bell and clapper made of perfectly elastic materials make any sound?
Equivalence? Textbook treatments of relativity sometimes illustrate the "equivalence principle" with the example of a person in an elevator. The elevator cable breaks and the hapless occupant falls with the elevator, experiencing a "weightless" condition in which he floats freely in his elevator frame of reference as if there were no external forces acting. Textbooks often say that the person inside would be unable, by any experiment, to determine that there was a gravitational field in his elevator. This example is, of course, flawed, for with sensitive instruments a person in the elevator could detect the gravitational field. How?
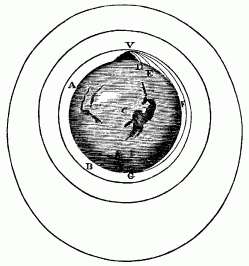
Ellipse or Parabola? Physics textbooks spend much space discussing trajectories of projectiles in the earth's gravitational field. These obey the law d = v_ot + ½gt², which is the equation of a parabola. But Newton tells us that the path of a cannonball (in the absence of air drag) is a portion of an ellipse with the center of the earth at one focus. The famous picture "Newton's mountain" illustrates this.
So if you were asked "What is the path of a projectile, an ellipse or a parabola?", which answer would you give? Resolve this apparent contradiction.
Newton's third law says: If body A exerts a force on body B, then body B exerts and equal and oppositely directed force on A. Newton's other laws would be useless without this important law. Newton's laws are said to be universal, applying everywhere and at all times. But Newton's third law cannot be correct in all cases, even in classical physics. Show why, with a simple example.
Newton's law of gravitation, F = GMm/R² is accepted without question by freshman. But a little thought reveals that it cannot be true in all cases. When R = 0 the force becomes infinite, an unphysical result. Give an argument why that is not a serious issue.
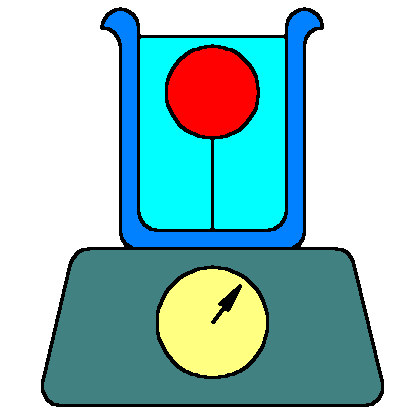
Floating idea. A beaker of water sits on a scale used to measure its weight. A ball, less dense than water, would normally float on the water. But it is tied down, completely submerged, by a string fastened to the bottom of the beaker. The ball is surrounded by water and does not touch the beaker walls. The string obviously exerts and upward force on the bottom of the beaker. The string breaks, and the ball rises to the surface, floating there. The string no longer exerts that upward force on the beaker. Does the scale now read more, less or the same as before? Support your reasoning with a free body diagram.
Holey physics. Physics problems are often framed with highly idealized situations. Here's a classic problem of that kind. If a straight hole were drilled all the way through the earth right through the earth's center, and a stone dropped down the hole, how long would it take to return?
To keep this simple, ignore the fact that the hole could not be drilled through the hot material in the earth, and if it were, it would fill immediately with magma. Then there's the pesky complication of the earth's rotation, so we must halt that, for the stone would collide with the wall of the hole. Which wall, by the way? Drilling the hole along the N-S rotation axis of the earth would be one way to avoid this issue.
To complete the idealization, assume the earth's density is homogenous.
And to extend the problem, after you have found the previous answer, suppose that a straight tunnel were drilled from New York to San Francisco. Now install a railway track through the tunnel. How long would the trip take in an unpowered railroad car, without being given any push, neglecting friction, etc.?
As usual we seek the simplest solution, preferably not even requiring calculus.
Forever is a long time. On an infinite frictionless plane could a perfect cylinder, given an initial push, roll forever?
Friction is a drag. Students sometimes suppose that friction always opposes a body's motion, tending to reduce its speed. But there are many everyday examples showing that friction can be necessary to initiate and sustain motion. Give some examples. State the definition of friction so that it cannot be misinterpreted.
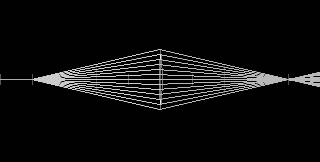
Racing photons. Consider light passing through a converging lens from a point source to a point image. The light rays passing through the lens near its edge must travel a greater distance from source to image than do the rays passing through the center of the lens. Wouldn't this make the rays arrive at different times and possibly cause destructive interference at the image? Explain.
Unweaving a spectrum. Sir Isaac Newton (1642-1727) is famous for his experiments with light and prisms. He showed that the light passing through a prism separates (disperses) into a colored fan (spectrum). He also showed that if that colored light is then passed through another prism, properly arranged, it can be recombined into white light. Thus, he argued, the colors are actually in the white light, not created by the prism. Here's a gallery of examples from the web, supposed to illustrate this experiment.

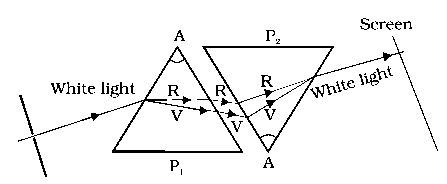
Textbooks and web pages frequently illustrate this experiment with such pretty pictures—and get it terribly wrong! Google prism recombine white light and view the images. Most of the images will be wrong in one or more serious ways. This is a telling example of why the web is called "the misinformation highway", for it is dangerously compromised by potholes. If you tried to duplicate this experiment in the lab, following these examples, you would surely fail. Identify the errors in each of these. What is a correct way to decompose white light into colors and then recombine it into white light? There are several ways.
I once had a student who wanted a project for extra credit to raise his unimpressive average. I suggested he go into the lab and duplicate this experiment. He copied textbook illustrations and failed every time. He was frustrated. Finally I suggested he might find out where the college library was, then locate Newton's "Optiks". There he found out one way to do it successfully.
The Soda Can. Here's a puzzle from Martin Gardner's collection. It is an old problem, but the method is still instructive.
Assume that a full cylindrical can of soda has its center of gravity at its geometric center, half way up and right in the middle of the can. As soda is consumed, the center of gravity is initially lowered. When the can is empty, however, the center of gravity is back at the center of the can. There must therefore be a point at which the center of gravity is lowest.
Knowing the weight of an empty can and its weight when filled, how can one determine what level of soda in an upright can will move the center of gravity to its lowest possible point?
To devise a precise problem assume that the empty can weighs 1.5 ounces. It is a perfect cylinder and any asymmetry introduced by punching holes in the top is disregarded. The can holds 12 ounces (42 gram) of soda, therefore its total weight, when filled, is 13.5 ounces (382 gram).
Reverse Osmosis. A correspondent from New Zealand sends us this ingenious idea that he saw in the Dec. 1971 Scientific American Amateur Scientist column. We'll let him describe it:

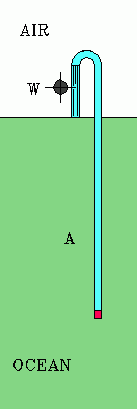
Osmosis is a process where water flows through a semi-permeable membrane from a less concentrated to more concentrated solution. Reverse osmosis is where water flows through the membrane from a strong solution to a weak one. Of course you must have pressure behind the membrane to make it flow the "wrong" way. To get fresh water to flow from seawater through a membrane takes a pressure of about 20 atmospheres. This is the basis of desalinating devices used on large ships.
Anyway, what you do is get a very long pipe with a semi-permeable plug in the end and fill it with fresh water and lower it over the side of a boat so that one end is a few metres above the surface and the other with the plug is at the bottom at the deepest ocean trench you can find�say 12 km down or however deep the ocean gets. Now, at this depth the head of salt water in the ocean around the end of the pipe is more than 20 atmospheres, say 21 atmospheres, so fresh water flows out of the ocean salt water into the fresh water pipe. The fresh water will rise about 10 m (21 - 20 = 1 atmosphere) above the surface somewhat like an artesian well. You may have to adjust the depths a bit depending on the density of the sea water but the principle seems plausible.
Not only will this device give an endless stream of fresh water but can be used to run a small generator.

The figure shows the tube in the ocean, its top end curved to direct water to the little water wheel, W. You've gotta love perpetual motion proposals that are so simple, with no moving parts, and hold promise of solving our world energy problems and our fresh water resource problems as well. That is, if only we can get enough of these machines running at once.
Pressure in the ocean varies linearly with depth, increasing by about 1 atmosphere for each 10 meters of depth. So the pressure in the ocean at a depth of about 200 meters (700 feet) is 20 atmospheres above atmospheric pressure. This fact may or may not be helpful.
This seems to be a great idea. But it won't work. Why not? An answer is given in the April. 1972 Scientific American, but it is a bit indirect. See also the June 1971 issue.
Which egg is boiled? This is a very old problem. Two eggs are on the table, one is fresh and one has been hard boiled. How can you determine which is boiled without breaking their shells?
Which is hollow? Two spheres have the same diameter, weigh the same, and are painted the same color. One is solid, of lightweight material. The other is a hollow shell made of denser material. Without damaging them, how can you tell which is hollow?
An attractive puzzle. This puzzle is often criticized for perceived ambiguity. Here's a version with most of the ambiguity removed.
You are given two iron bars, identical except for the fact that one bar has been magnetized, the other is not magnetized. Using nothing other than the two bars and your hands, how can you determine which is the magnet? We will allow gravity to operate as usual on you and the bars."
Carelessly worded versions of this problem lead to answers such as these:
1. Suspend one by a thread tied around its center and observe whether it tends to point north.
2. Heat one of the bars very hot and let it cool. If the bars no longer attract as strongly, then the one you heated was the magnet.
3. Drop one repeatedly on the floor. If the attraction between the bars is reduced, then the one you dropped was the magnet.
But we ruled these out by specifically requiring that you must use only the bars and your hands. No string or wire can be used, no other metal, and nothing to heat a bar. You can't even use the magnetic field of the earth. So what is the simplest way to identify the magnetized bar?
One answer, well known, is the "T" test. Place the bars touching in a T configuration, with the end of one at the center of the other. If they attract, then the one which is the upright of the T is the magnet, for the other has its poles at either end and no pole at its center.
But magnets of high permeability materials can be made with many poles, for example one with a [N SS N] arrangement. Such a magnet would not tend to point north when suspended and might fail the "T" test. What's the simplest way to identify the magnet, no matter how that magnet's poles are arranged?
Which is longer? Prepare two metal tubes. Mine are cut from 1 inch diameter aluminum tubing from the hardware store. One tube is 11 inches long. The other is 1/4 inch shorter. Try to ensure that the tubes have no scratches or imperfections that could distinguish one from the other.
Hold them up, one in each hand, and ask if anyone can visually see that one is shorter than the other. Of course no one can. Hold them side by side, touching, and the difference is obvious. Ask someone to take them, then turn around to hide them from your sight, choose one, and then hand it back to you. You pretend to judge its length between your hands, touching the tube at its ends, only with your fingertips. Set it aside and ask for the other, doing the same, then announce "This one is (shorter/longer as the case may be)."
You could do this blindfolded, but that's probably overdoing it for a physics demo. What is your secret?
Rolling paradox. Physics textbooks define the force due to friction as a force tangent to two surfaces at their point of contact. Consider a ball or cylinder rolling without slipping on a perfectly flat and level surface. We expect it to slow down. We naively assume that friction is the reason it slows down, eventually stopping. Certainly the friction is opposite to the ball's velocity, and would therefore decelerate the ball's motion by Newton's second law. But that force due to friction has a torque, and this vector torque around the center of mass of the ball is in the same direction as the ball's angular velocity vector. This would increase the ball's angular velocity, making it roll faster and faster. Resolve this apparent contradiction.
When inventors first proposed railway transportation, using steel wheels on steel rails, some skeptics said "The wheels will just spin in place, and the contraption won't go anywhere." Maybe this paradox was in their minds.
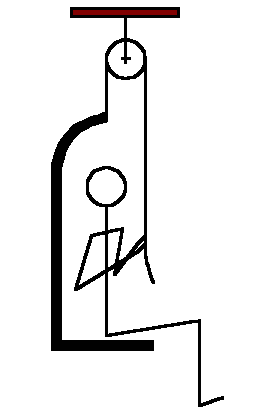
The bootstrap principle. The tall tales of Baron Munchausen include the story of his narrow escape from a sticky situation when he was mired in a bog. The resourceful Baron reached down and lifted himself up by pulling on his bootstraps. We know that is impossible, but can a person, using physics and a pulley system, lift himeself using only his own strength?
Consider the system shown. A lightweight chair is used, with an overhead pulley. Can this work? Are there any limitations on this system? Show the vector analysis with free body diagrams.
At rest. Rare is the physics book that doesn't say something like "The net force on a body at rest is zero" in the chapters on statics. And it also says that if the net force is zero, the acceleration of the body is zero. Then, in the dynamics chapters, we may see "A body thrown straight upward is momentarily at rest at the highest point of its trajectory". The student then logically concludes that at that point the net force on the body is zero (at least for an instant) and therefore its acceleration at that point is zero. This is the "at rest → zero net force → equilibrium → zero acceleration" fallacy. Can we blame students for taking textbooks at their word?
Can you resolve this apparent contradiction?
Lost energy?

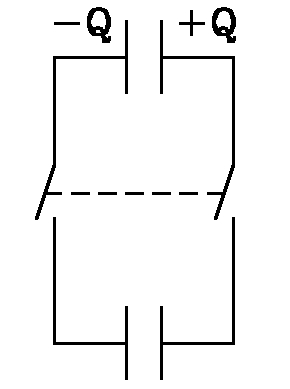
The capacitor paradox.
This capacitor paradox has been discussed on the web and in published papers, yet people still argue about it.
Obtain two identical capacitors. Charge one of them. Then connect them together so that the charge is shared equally by both. A simple calculation shows that the energy of the two charged capacitors after this operation is only half that of the single initially charged capacitor. What happened to the lost energy?
Of course, one immediately suspects that energy is lost by heating the connecting wires. So we idealize the problem and use resistanceless connecting wires. Still, we must consider energy radiated away by the accelerating charges during the initial process of closing the switches and in the subsequent acceleration of electrons during the redistribution of charge. Yet published papers argue about the details of these processes.
So what's going on? Is circuit theory and classical electromagnetic theory wrong? Can you resolve this simply?
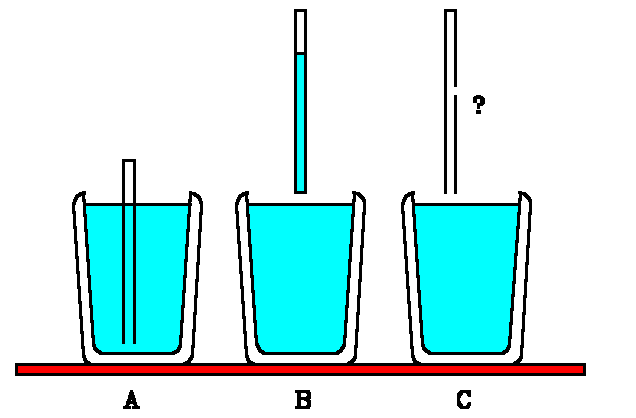
Grasping straws.
1. We have all done this demonstration, using a drinking straw and a glass of water. Insert the straw in the water (A), close off the top of the straw with your finger, then raise the straw, keeping the top closed. This lifts a column of water inside the straw (B) in spite of the open end. What physics is being demonstrated?
2. We do not normally look at details of this simple demonstration, but what about the lower end of the straw? There's a surface of water there, exposed to the air. What is its shape?
1. It bulges downward.
2. It bulges upward.
3. It is nearly flat.
Support your guess with a valid physical argument.
3. Now let's make it more interesting. Make a hole in the drinking straw at about two inches from the bottom. Make the hole as large as the end openings of the straw. Now immerse the straw in the water glass. The side hole must be below water level. Now close the upper end of the straw with your finger. Lift the straw until it is entirely out of the water (C). What do you predict will happen? Support your answer by an argument based on physical laws. Specifically discuss what's going on at the side hole. Now try it.
A slippery slope. If you are descending a slippery slope in a car, would you retain better steering control if your front wheels or your rear wheels locked up?
Powerful magnets? One often hears strong magnets described as "powerful". But are they a source of power? I often hear people argue that magnets must be an inexhaustable source of power. They cite the lowly refrigerator magnet, saying "It supports its own weight on the wall of the refrigerator forever, or at least for many years. So magnets must be a source of considerable energy." I hear this frequently from people who think they can devise a perpetual motion by arranging magnets in a rotating mechanism to extract their stored energy.
What is wrong with their argument?
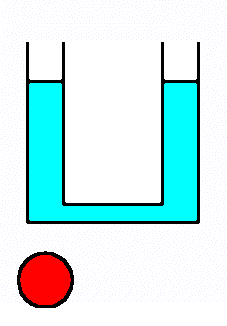
Gravity enhancement. Henry Cavendish (1731�1810) measured the force of gravitational attraction between two lead balls in a laboratory setting. He used a sensitive torsion suspension to measure such a small force. Suppose we have a liquid in a U-tube, in equilibrium, and then place a heavy lead ball (red) just under the left side of the tube. How will this affect the liquid levels in the tube?
Negative reaction? Usually when we pull on something it moves toward us in the direction of the applied force (unless it is nailed down). Can you think of, or devise, a simple system that moves away from you when you try to pull it toward you?
Foucault's pendulum.

Foucault pendulum at the Panth�on in Paris.
Léon Foucault (1819�1868) installed a large pendulum in 1851 at the Panthéon in Paris, to demonstrate that the earth rotates. It was 220 feet long with a 62 pound bob. When set swinging it slowly precessed because it maintained its initial plane of swing while the earth rotated underneath it. This was easily observed over the course of a day as its plane of swing changed with respect to the floor underneath it. Science museums around the world have such pendulums, and some university physics buildings do also.
But why does the pendulum maintain its motion in the original plane? After all, its suspension wire is attached at the top, and surely the rotation of the building will exert a twisting torque on the wire. Wouldn't this cause the pendulum's motion to follow that of the building it is in? Some explanation is needed.
Then there's the question of initial conditions. When the pendulum bob is pulled back in the morning and released, this process is done in an already rotating reference frame—the building itself. Shouldn't this initial motion bias the pendulum to retain that motion for the rest of the day, so its plane of motion wouldn't change at all with respect to the building? Therefore no apparent precession would be observed.
As a university student I was once given some good advice about physics. "Do you understand all you know about it?" These simple questions posed by the Foucault pendulum nagged me many years before I discovered the answers. Textbooks and professors avoid this by seldom raising such questions.
Going around in circles. Mankind, sometimes called "a crawling disease on the face of the earth", affects the earth in many ways. But one effect of human activity is seldom mentioned. In most countries automobiles travel on the right side of the road. Traffic circles are traversed counterclockwise. Most automobiles and trucks return home after they take a trip, so their motion is net counterclockwise. In the USA carnival carousels (merry go-rounds) also turn counterclockwise, and races, human, horse, dog and auto, are run counterclockwise. One exception is Great Britain (and a few other countries), where all these go clockwise, including auto traffic and roundabouts.
Does this rotational motion on earth's surface alter the rotation speed of the earth, if only just a smidgen? Might this speed up or slow down the earth's rotation? Should we be concerned? And what is the effect of all those earth satellites we have put into orbit, most of them launched toward the east?

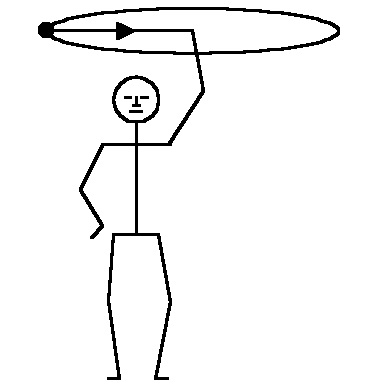
Illustrating centripetal force.
A circular argument. A ball is on the end of a string. Holding the other end of the string you swing the ball in a large circle. Textbooks often present this as a problem, asking you to relate the angular speed of the ball to the string tension, using the well known formula for centripetal force, F = mω²R. But is the tension really equal to the centripetal force?
Due to air resistance the ball will slow down. To keep it going something else must supply energy in the form of work. But if the string is radial, and the ball's motion is tangential to its circular path, the force and displacement are perpendiclar to each other. So how can the string do any work on the ball to sustain its motion?
Pendulum perplexity. Every physics textbook tells us that the period of a simple pendulum does not depend on the mass of the bob. But these books rarely address the question "Why is the period independent of mass?" If you follow the derivation of the period formula you will see that the mass drops out of the calculation. But there's an easy and insightful way to prove this without even doing mathematics. Can you?
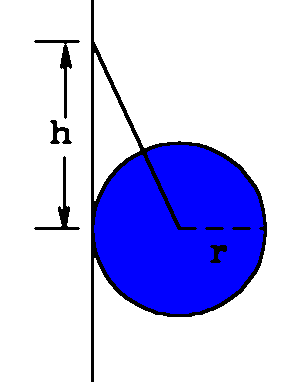
Leaning ball. A uniform sphere of mass m and radius r hangs from a string against a smooth, vertical wall, the line of the string passing through the ball's center. The string is attached at a height h = √(3r) above the point where the ball touches the wall. What is the tension T in the string, and the force F exerted by the ball on the wall? If the ball is rough, with coefficient of static friction μ_s, how are these forces increased or reduced?
Action and reaction. Textbooks often tell us that Newton's law is somthing like "For every action there is an equal and opposite reaction." Of course this is carelessly worded. How can any two things be equal and opposite? One should say: "For every action there is an equal size and oppositely directed reaction."
But what is the definition of "action"? One might argue that "reaction" is a negative "action". If so, the original statement might be correct, but it is still confusing. Seriously, when you have an action/reaction pair how can you tell which is the action and which is the reaction?
Putting the cart before the horse. A horse is hitched to a cart. The horse exerts a forward force F on the cart and the cart exerts the same size force backward on the horse by Newton's third law. So the horse and cart will not go anywheree.
What is the flaw in this argument?
Lunar attraction. Standing on the earth, are you closer to the sun at high noon at the time of new moon, or at high noon a half month later at the time of full moon? Why?
Going around in circles. The Ptolemaic model of the solar system was geocentric (earth centered) and based entirely on circles (which were considered the perfect figure). To agree with observations of planetary positions, it became extremely geometrically complex, with circles (cycles) and smaller circles (epicyles), deferents and equants and other gimmicks to make it agree with observation.

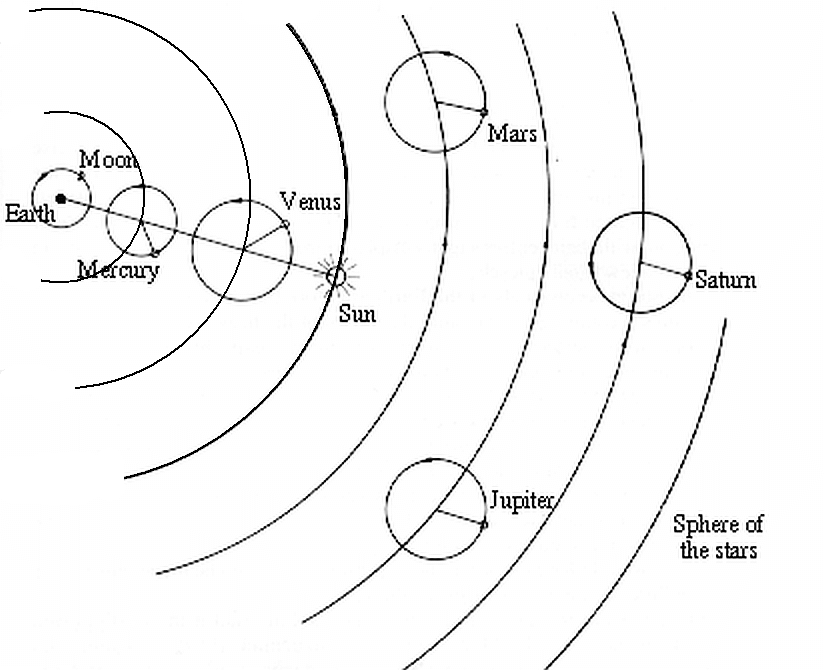
The Ptolemaic system, simplified. Not to scale.
Adapted from Van Allen, James A. 924 Elementary Problems
and Answers in Solar System Astronomy. U. of Iowa Press, 1993.

Copernicus attempted to simplify this, using a heliocentric (sun centered) model. But he still insisted on a geometry based on circles. His system still needed epicyles, but, he claimed, fewer of them. Less important than the number of epicycles is a property of the particular epicycles that his system eliminated. Six of the abandoned cycles and epicycles had, in Ptolemy's system, one important thing in common. What was it?
The persistent bug. An infinitely stretchable elastic band connects a tree with the rear bumper of an automobile. As the auto moves away with constant speed the band stretches. A bug on the band crawls slowly toward the auto. Can the bug ever reach the auto, given enough time?
The holey sphere.

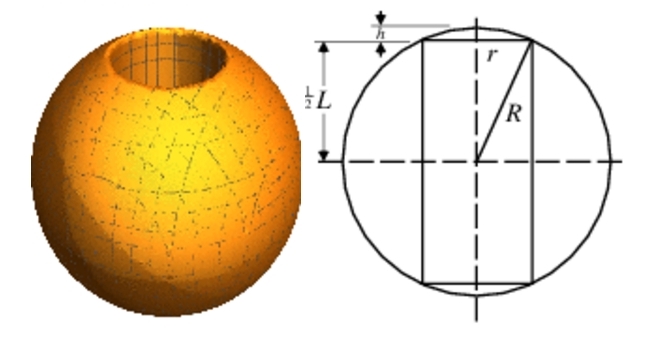
The holey sphere. L = 6".
From mathworld.wolfram.com.
Browsing Martin Gardner's books I stumbled on this diabolical puzzle. Gardner calls it "an incredible problem". He traces it back too Samuel I. Jones' Mathematical Nuts, 1932, p. 86.
It is seen on the web in various forms, often ambiguous in wording, along with endless discussions often leading nowhere. I have tried to restate it to remove ambiguity (which isn't easy).
A hole is drilled completely through a sphere, directly through, and centered on, the sphere's center. The hole in the sphere is a cylinder of length 6 inches. What is the volume of the remainder of the sphere (not including the material drilled out).
You'd think there's not enough information given. But there is. The solution does not require calculus. Gardner gives an insightful solution that requires only two sentences, including just one equation.
Oblate earth. Due to its rotation, the earth isn't spherical. It is an oblate spheroid, bulging at the equator. Is its radius of curvature greater at the equator or at the poles?
The resistor chain.

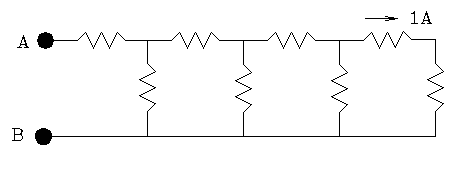
The resistor chain.
Each resistor in this chain has resistance of 1 ohm. A power source is connected to the terminals A and B. The current in the rightmost two resistors is 1 ampere. What is the potential difference across the input terminals A and B of this chain? What is the resistance of the entire chain as measured at points A and B? What current does the power source supply to this circuit?
This problem is straightforward, though tedious, for the chain has only four "links". It isn't worthy of the label "puzzle". But what if the chain had 500 links? Extending the chain further is of no practical use, but it makes a nice puzzle to solve it for an infinite number of links, for a surprising pattern develops as you work it out.
Hint 1: Sometimes it helps to solve a puzzle if you approach it from the other end.
Hint 2: Sometimes it doesn't.
Hint 3. How might this relate to Fibonacci?
Skinning a catenary. A power cable is strung between two utility poles. Of course, it sags, in the shape of a curve called a catenary. At each end where it is attached to a pole, the cable makes an angle 10° to the horizontal. The weight of this section of cable is W. What is the tension in the cable at its lowest point? What is its tension at each of the poles?
Finding a center.

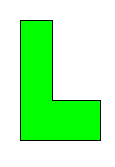
Fig. 1. Find the
center of mass.
Fig. 1 shows an L-shaped flat sheet of metal of uniform thickness and composition. Can you find its center of mass, using only an unmarked straightedge?
Falling Slinky. Suspend a Slinky ™ spring from one end. If you release that end, how will the spring fall?
1. The entire spring falls, retaining its stretched length until the lower end hits the floor, then the rest of the spring falls, compressing as it goes.
2. The entire spring falls, compressing as it goes.
3. The lower end rises to meet the upper end, then the spring falls in compressed state.
4. The lower end maintains its position until the rest of the spring compresses, then the spring falls in compressed state.
Follow-up question: What is the initial acceleration of the upper end of the spring as it falls?
1. The acceleration due to gravity, g
2. An acceleration greater than g.
3. An acceleration less than g.
And another question: If a weight were attached to the bottom of the suspended slinky, how would that affect our previous answers?
Oh, just one more thing: If the spring constant or speed of compression pulse in the spring were different, could the lower end rise briefly just after the upper end of the spring is released?
As always, explain your answers.
Snap!. We all know how to "snap" our fingers, which is easier to do than describe in words. Press the thumb and middle finger together forcefully, letting the finger slide suddenly off the thumb, and you will hear a snapping sound. Without doing it, explain exactly where the sound comes from.

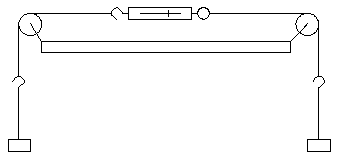
Tug of war.
Tug of War. Two equal weights, W, are arranged as shown, An old-fashioned spring balance is connected in the middle of the horizontal cord, and is supported so that it does not cause the cords to sag. (Perhaps, use a weightless spring balance.) What is the approximate reading of the spring balance?
1. 3W
2. 2W
3. W
4. Zero
5. W/2
15 puzzle magic squares.

Wooden 15 puzzle.
The classic "15 puzzle" is still found in toy stores. It consists of square tiles numbered 1 to 15 in an enclosure 4×4 tiles in size. When filled there's one empty space, allowing tiles to be shuffled into different orders. Typically one tries to get the tiles in numeric order left-right by sliding them, never lifting them from the box.
Puzzle master Sam Loyd claimed he invented this toy in 1891, but he wasn't the first with the idea. Noyes Chapman applied for a patent on it in March 1880. Loyd did describe a prank one can play with it: just interchange two tiles so that it cannot be solved into numeric order left-right. He called it the 14-15 puzzle because he interchanged those two tiles, but interchange of any two tiles would have the same result. The puzzle could still be solved by devious methods.
```
 1   5   9  13
 2   6  10  14
 3   7  11  15
 4   8  12
```
Or turn the puzzle sidewise:
```
 4   8  12 
 3   7  11  15
 2   6  10  14
 1   5   9  13
```
But there are more opportunities for puzzles. Can you shuffle the tiles of the standard 15 puzzle to make a "magic square" in which the tiles in each row, column and diagonal sum to 30?
Speedy eclipse. Seen from above the earth's north pole, the earth revolves around the sun counter-clockwise. The moon orbits the earth counter-clockwise. The earth spins on its axis counterclockwise. Then why does the region of totality of a solar eclipse move across the earth from west to east? For example, in the U.S. solar eclipse of 2017 the totality region arrived on the West Coast in Oregon about 1.5 hours later was seen on the East Coast in Charleston, S. C. Check your answer by calculating the time it took the region of totality to cross the U.S.A.

Slip or slide?
Slip or slide? Imagine that a new process can produce perfectly frictionless solid materials. A solid cylinder is placed at the top of an inclined plane, both made of this material. The cylinder is released, being careful not to give it any push or rotation. Will the cylinder roll down the plane without slipping, or will it slide down the plane without rotating? Or will it both slip and slide?
A seasonal puzzle. In the Northern hemisphere, summer is warmer than winter. Why? The usual superficial answer is, "Because the earth's axis has a fixed direction in space, and in summer it tilts toward the sun, but in the winter it tilts away from the sun." That's true but isn't a complete answer. Two important processes aren't mentioned. Can you explain why the tilt affects the seasonal temperatures?
Curious attraction. Those business cards with magnetic backs present an interesting puzzle. Their black backs have alternating strips of N and S magnetic poles, spaced 1mm apart. You can test this with two identical cards. Place them face up, stacked, move them along their length and they move smoothly. Move them perpendicular to their length and the movement "jumps" as you go from N to S magnetized strips. Turn them so their black sides are in contact, similar results are seen. But... Rotate one with respect to the other (black surfaces still in contact) and at angles of 10° through 90° the motion is smooth, and continues to be attractive even with the cards at 90°. Why should this be, since at 90° there should be as much attraction as repulsion, and you'd expect the cards would not attract?
These magnets are called zip magnets. The magnetic elements in them are in a Halbach array. Here are some web links may help you visualize their behavior, but they don't give the answer to this puzzle.
Physics Central. Zip magnets.
EngineerDog.com. Why do refrigerator magnets only stick on one side?
No one has supplied an answer yet.
Armagedon. If we detected (soon enough) a large space rock headed for a collision course with earth, and we wanted to prevent it, which is the better strategy?
1. Send up a large rocket to push the rock opposite to its velocity to slow it down.
2. Send up a large missile with a nuclear warhead to land on the rock and blast it to smitherines.
3. Send up a large missile with a nuclear warhead to land on the rock and detonate, to push the rock off course.
4. Send up a large rocket to push the rock sidewise (at right angles to the rock's velocity) to deflect its course.
Why would this work? How would its chance of success depend on the mass and relative speed of the rock?
A cloudy mystery. We have all seen clouds of many kinds, wispy clouds, hazy clouds, and fluffy cumulous clouds. Cumulous ones take many shapes, but maintain an individuality as you watch them from the time they form till they dissipate. Why do they persist so long? They consist of water droplets, which are heavier than air. Why don't these just spread out into a uniform haze covering the entire sky? What holds clouds of water vapor together into defined (though slowly changing) shapes for so long? How do they form "out of thin air" in the first place? What's the physics of it?
You might compare clouds of steam from a tea kettle, or an old fashioned steam locomotive as you search for an answer. Or smoke from a smokestack.
Hot air. Somewhere in your answer to the previous problem you may have asserted that "hot air rises". This raises a fundamental question, "Why does hot air rise?" Simplistic textbook explanations assert that the air near the flame expands, and is therefore less dense, and lighter things rise in denser fluids. Does this really explain the process? Why does the heated air behave like a volume of lower density than the surrounding air?
Consider a hot object, like a lighted match or candle. Smoke immediately rises from it. But why don't the air molecules heated near the flame simply move out in all directions up, down and sidewise equally? What biases the molecules to move preferentially upward?
Of course, heated molecules move faster on average, and soon interact with other molecules, exchanging energy and momentum. What, in this process, biases them to move upward? Any explanation on the molecular level must include gravity.

Return to Donald Simanek's front page with the full menu,
Return to puzzles with answers. Answers to the puzzles on this page.
Return to the main page of physics puzzles..