Flat Plate Pendulum.

Every freshman student knows that the period of a simple pendulum does not depend on the mass of its pendulum bob, but probably doesn't know why. This is something we'll have to look into sometime. Readers are invited to send me their own arguments for this. Simple answers are preferred.

But this idealized swinging point mass is a bit unrealistic. Increase the size of the bob and you get a slighty different result. If the swinging object is of considerable size, the result can be very different, and this is called a "physical pendulum". Calculations of their behavior can be considerably more complex.

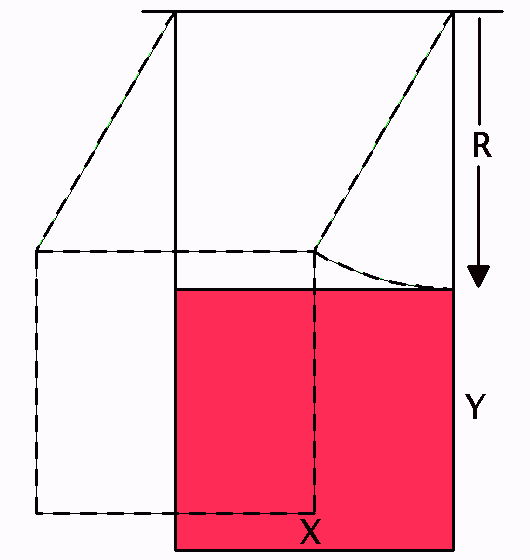Consider this physical pendulum. It consists of a square flat plate (red) of mass M and dimensions X and Y, suspended by its upper two corners with two strings of length R from a fixed support. It swings in a flat plane, the plane of the diagram, suggested by the dotted line image.

Calculate its period.

Answer.

The simplest way to "see" this result is to note that each and every piece of the plate swings in an arc of the same radius. That's a geometric result of the parallel string suspension. Imagine all these pieces separated, swinging in synchronism. Each would have period T = 2π√(R/g) where R. So the entire plate has that period.

In fact, an object of any shape suspended from two parallel strings of equal length has the same period. And any solid shape suspended from four parallel strings of equal length does also. Such parallel suspension ensures that the object swings, but does not rotate.

But if the suspension strings are non-parallel, some interesting motion results. A flat plate, suspended that way from its four corners can swing with a rocking motion. Definitely not elementary. In fact this could easily lead us to situations of gentle rocking as in the piece of furniture known as the platform rocking chair.