The Soda Can.

Assume that a full cylindrical can of soda has its center of gravity at its geometric center, half way up and right in the middle of the can. As soda is consumed, the center of gravity moves lower. When the can is empty, however, the center of gravity is back at the center of the can. There must therefore be a point at which the center of gravity is lowest.

To clear your mind of trivial and uninteresting details, assume the can is a perfect cylinder. Knowing the weight of an empty can and its weight when filled, how can one determine what level of soda in an upright can will move the center of gravity of can and contents to its lowest possible point?

To devise a precise problem assume that the empty can weighs 1.5 ounces. It is a perfect cylinder and any asymmetry introduced by punching holes in the top is disregarded. The can holds 12 ounces (42 gram) of soda, therefore its total weight, when filled, is 13.5 ounces (382 gram). We simply take the height to be H, and our results will be a fraction of H.

Answer and discussion.

[Eq. 1]

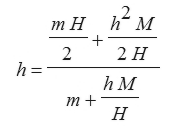
If you graph the center of mass as a function of h, you get a curve that has a minimum at exactly h = 2.5.

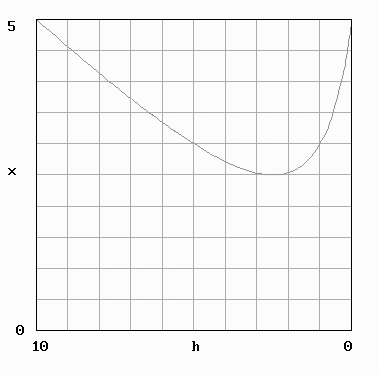Center of mass, x, as a function of height of liquid in can, h. The can height is 10 units.

Notice from the graph that when the center of mass is at its lowest point, it is also exactly at the liquid surface. Is this a general result?

As the liquid level lowers, the center of mass of the system is at first within the volume of the liquid. But the lower it gets, the closer the center of mass moves to the surface of the liquid. At some point it is exactly at the surface of the liquid. As the liquid level lowers more, the center of mass rises and eventually reaches the center of mass of the can when the can is empty.

When the center of mass is exactly at the liquid surface, adding more liquid will raise the center of mass, for that liquid goes above the previous center of mass. But taking away liquid will also raise the center of mass by removing weight below the previous center of mass. So this is the critical condition when the center of mass is lowest. Therefore the answer is that the center of mass is lowest when it is at the same height as the surface of the liquid.

This is, perhaps, the most profound and useful fact about this problem, for our argument for it did not depend on the shape of the can. Therefore it also applies to containers of any shape.

But this is probably not the form of answer we wanted. We also want to know the location of that critical point in relation to the height of the soda can.

Using the notation above, we can equate the moments of liquid and can.

[Eq. 2]

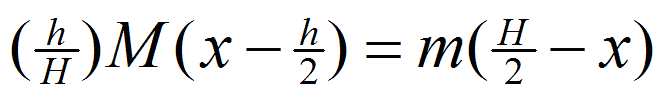
When x = h we get a quadratic equation:

[Eq. 3]

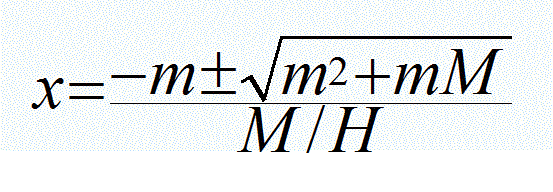
Discard the physically meaningless negative root. This reduces to:

[Eq. 4]

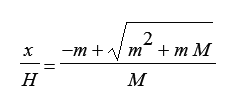
Substituting values, we get x = 2.5 for a can of height 10. That is 1/4 the height of the can. That simple fraction is a result of the ratio of the mass of the can to the mass of its contents when full. Other mass ratios do not give simple fractions.

Now (2016) empty aluminum 12 oz soda cans weigh about 0.5 ounce (14.7 gram). One wonders whether the person who invented the problem chose 1.5 ounce to make the arithmetic easier. Or maybe the problem dates from an earlier time when the cans were more nearly cylindrical and weighed three times as much as they do now. With today's lighter cans, the lowest center of gravity of the partially filled can is H/6.

A lengthy discussion of this can be found in Norbert Hermann, The Beauty of Everyday Mathematics (Springer-Verlag, 2012). A straightforward calculus solution is also included there. It is too lengthy to show here.

The calculus solution begins with a general expression (Eq. 1 above) for the system center of mass, x, as a function of the amount of liquid in the can (or the height of liquid in the can, h. Then set dx/dh = 0. Solve the quadratic equation to find the minimum value of x. This is a lengthy and messy solution. You may need to use L'Hospital's rule.

These web documents use intuitive approaches.

Martin Gardner Physics Stumpers.

Problem #71.