Touchy equilibrium.

The balanced wheel.

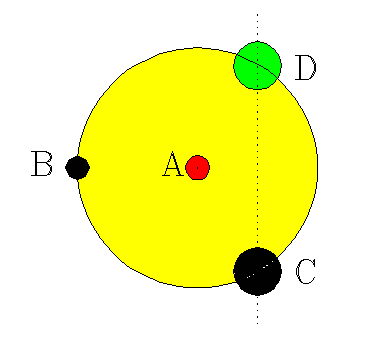
A wheel (yellow) is free to rotate about its axle (red). A weight W (black) is fastened at B, a distance R from the center of rotation. A weight 2W (black) is fastened at a point C that would place it at distance R/2 from the vertical axis through the center of rotation.

Clearly the wheel with these two weights has balanced forces and torques. But if the weight at C were relocated to point D, the torques and forces would still be in balance.

A system can have balanced forces and torques yet be in unstable equilibrium. The slightest nudge would then cause the system to move away from that position. If it were in stable equilibrium a nudge would displace it, but it would return to the stable equilibrium position.

So which of the positions B and C are stable? The naive answer is that position C is unstable because it would make the system "top heavy". But that is a vague colloquial concept, not a physical principle. Can you give a physical argument to settle this question?

Answer

At a position of stable equilibrium, the system center of mass is at a position of relative minimum height. Movement of the system in any direction raises the height of the center of mass.

Forces and torques add linearly, so superposition principles may be applied.

If the wheel is pushed by an exernal agent to rotate counter-clockwise a tiny amount, lowering mass A by Δy, mass B is raised a height Δy/2. This alone does not change the system center of mass. But the displacement of the wheel also moves mass B to the right horizontally, increasing its lever arm. This increases the clockwise torque on the wheel, opposing the torque that pushed the wheel.

If the wheel is nudged (pushed) to rotate clockwise, this raises mass A. It also moves mass B to the left horizontally, decreasing its lever arm. This increases the counter-clockwise torque on the wheel, opposing the torque that pushed the wheel.

In both cases when the external agent quits pushing the wheel, the wheel returns toward its equilibrium position, oscillating about that position until it comes to a stop in static equilibrium.

If the same analysis is applied to the case with the mass 2M at position C, you will find that position to be unstable. This is left as an exercise for the reader.

Return to Physics puzzles.
Return to the Donald Simanek's home page.