The windup perpetual motion chain.

Bessler's Belts.

Johann Bessler (1680–1745), a.k.a. Orffyreus, compiled a book Machinen Tractate containing pictures of an astounding variety of perpetual motion devices known at his time. Among them we find this small woodcut of three curious devices.

These are easily overlooked in Bessler's book, and they have received little comment. It seems they describe belts with weights passing over pulleys. In the first picture the weights are closely spaced on the right side, but on the other side they are much farther apart. If this were possible, there are more weights on one side than the other. Can this imbalance be maintained if the belt moves continually? What magic happens to decrease their spacing as they pass over the pulley?

In the second picture The weights seem to be larger on one side. In the third picture they have different shape on each side. [1]

Obviously these are unworthy of consideration as candidates for perpetual motion. But what if we could find a mechanism that would take widely spaced weight and scrunch them together as they pass over the belt? This would achieve continual weight and torque overbalance of the belt. Here's a proposal.

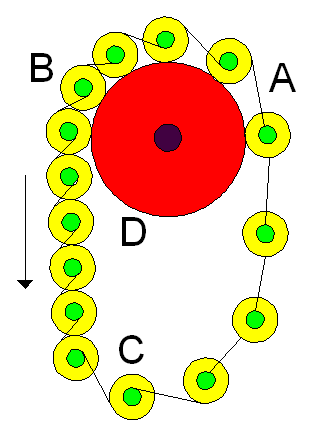The Windup Chain.

A chain of yellow/green spools is supported by a fixed red drum, D. They have gear teeth around their circumferences. These are not shown here—too difficult for me to draw. Each yellow weighted spool has a smaller coaxial pulley (green) rigidly attached and an outer attached pulley of larger radius (not shown explicitly). A stout string connects the inner and outer pulleys of adjacent spools and is attached to them.

As shown, the spools on the left side are touching and held together by the gear teeth. They got that way as the weight of pulleys hanging on the left pulled the chain counter clockwise around the fixed drum, D, winding up the strings connecting the adjacent spools. This windup process began at position A and was completed at position B. At point B the gear teeth are meshed, and the tension of the string and friction at the gear tooth faces holds them together. At the bottom, C, the tension decreases enough to allow the spools to separate. The teeth can be shaped to facilitate this, a minor engineering detail. Or, instead of gear teeth, the curved surfaces could be a rubberized material that grips, ensuring rolling without slipping. [2]

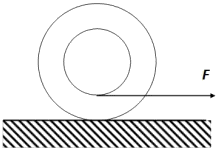The wheel rolls toward the hand pulling it.

As the spools move around the top of the fixed red drum, each one moves faster than the one ahead of it because of the ratio of pulley diameters cause the strings to wrap around the smaller (green) pulleys. This is like the physics demo of the yo-yo rolling on a flat surface, pulled by its string wound around its axle. If the string comes out from the bottom of the axle, the yo-yo rolls along a surface faster than the agent pulling the string. (I always wondered what practical application this toy might have.

The total hanging weight on the left is clearly greater than that on the right, and it will cause the chain to move from right to left around the drum, D. The chain is a closed loop, the lower part not shown. When pairs of locked pulleys reach the bottom of the loop, the tension on the connecting string is reduced, and the spools are free to unwind. The pulleys now have a separation more than twice that of the ones hanging on the left side.

The load on the left of the drum is, for example, twice that on the right. So there's a gravitational force imbalance, causing a net force that accelerates the belt's motion. The belt speed would increase continually, and some brake or load must be added to prevent it going fast enough to destroy itself. So the belt can continue to rotate forever. Ideally, a mechanism should be added to tap the belt's excess energy to perform useful work.

Will this work? If not, why not? Does it violate any laws of physics? If so, which ones?

The rules of the game are: You may assume friction is negligible wherever it would reduce system performance, but is present wherever necessary to facilitate the device's operation (as at gear tooth faces). If the mechanical advantage of a system is great enough it can tolerate some dissipative processes like friction and still have over-unity energy performance.

You might call this device "self-winding". Though this device isn't patented (yet), this picture of it is copyright June 23, 2019 by Donald E. Simanek.

Notes.

[2] This sort of mechanical detail, difficult to accomplish in practice, is seen in many perpetual motion proposals. For example, there are many proposals for buoyant belts that have a chain belt of balls that enter a tank of water near the bottom, and then buoyancy lifts them to the top of the water where they emerge and pass over a pulley to repeat the process. But how do you design a leakproof seal at the bottom of the tank that allows frictionless entry of the balls? (See: Buoyant engine #4.) In all cases I've seen, these mechanical difficulties are not the reason the device can't work. The fatal flaw of the idea lies elsewhere. Even if that mechanical detail were fixed, the device still wouldn't work. So I won't dwell on this detail here. Let mechanical engineers deal with it. The fatal flaw in this design also lies elsewhere.