P-1 CALCULATION EXERCISES
Instructor's notes and "solutions."
PRE-LECTURE
Assuming the students have read the assignment it will only be necessary to do for them a few new examples of mathematical operations with exponentials, and answer any questions they may have over the assignment.
If the students did not have the time or the materials to read the assignment, you will have to at least summarize the theory of exponential notation and significant figures. This may take half an hour of laboratory time.
ALTERNATE PROBLEMS
Three sets of problems are provided to be done during lab, A, B, and C. Section D has problems requiring library research, to be done as homework. The instructor may devise additional sets in the same spirit. These may be alternated in successive years, so students are less likely to use solutions of a friend who took the course the previous year.
LIBRARY RESEARCH
Request that students not check out the books they consult from the library. Other students may need to consult the same books.
ANSWERS TO PROBLEMS:
Express all answers in exponential notation in standard form, rounded to the appropriate number of significant figures.
(1) A classroom has dimensions of 5.8 meters, 10.2 meters, and 3.5 meters. Calculate the volume of the room in cubic meters.
Answer: 207.06 m3 which should be rounded to 210, to retain the first uncertain digit.
(2) Calculate the number of cubic centimeters in a cubic meter. (The answer is not 100.)
Answer: (100 cm/m)3 = (102)3 = 106
(3) Use the result of problem 2 to calculate the number of cubic centimeters in the room described in problem 1. Then check this answer by first converting the room dimensions to centimeters, then multiplying them together.
Answer: 207 x 106 cm3, or better, 2.07 x 108 cm2, rounds to 2.1 x 108 cm3.
(4) How many cubic centimeters are in a cubic kilometer? Since this is a large number, express it in exponential notation.
(102 cm/m × 103 m/km)3 = (106)3 cm/km = 1018 cm/km
(5) One light year is the distance light travels in one year. The speed of light is 2.9979250 x l08 meters per second. Express one light year in meters, to three significant figures.
One year = 3.156 x 107 seconds, so one light year is 3 x 108 m/s (3.156) 1 107 = 9.46 x 1017 cm = 9.46 x 1015 meters. About 10 million million kilometers. (In some rough, "back-of-the-envelope" calculations, the approximaate value π x 107 seconds/yr is used.)
Answer: 9.46 x 1015 meters. About 10 million million kilometers.
PROBLEM SET A
(A1) For expressing very large numbers, the unit duo has been invented by mathematicians. A duo represents the number 1 followed by one hundred zeros. A still larger unit, the duoplex is defined to be 1 followed by a duo of zeros. Express both of these units in exponential notation in an unambiguous manner. All of the numbers used in physics happen to be smaller than a duo.
1 duo = 10100, and 1 duoplex = 10(10100). Be sure that the student realizes that the parentheses are necessary, point out that the expressions (AB)C and A(BC) are not generally equal. Suggest that the student find a numerical case where they are not equal (choosing small integer values for ease of calculation).
Example: (23)2 = 64, but 2(32) = 512.
(A2) The radian is a unit of angular measure used in science and engineering. It is defined by the relation: 2π radians ≡ 360°. The smaller an angle becomes the more nearly is its radian measure equal to its sine. So, for small angles, one can approximate the sine function by using the radian measure instead. How small an angle is required for this approximation to be correct to three significant figures? To four significant figures? (Use a digital calculator or consult a good trig table to answer this.)
For angles less than 0.14 radian (8°) the approximation is good to three significant figures.
(A3) Find the sine of 0.0001 degree to four significant figures. How accurately can you determine this?
sin(θ) ≅ θ = (0.0001)2π/360 = 1.745 x 10-6
The accuracy is limited by the value of π used and the calculating device. The student also might suggest use of a power series expansion of sinθ, in which the accuracy is limited only be one's time and patience.
(A4) An article about prime numbers in the Scientific American magazine of March, 1964 mentions that "The Computer Division of Los Alamos has a magnetic tape on which 20 million prime numbers are recorded." Suppose we wanted to print all of these numbers in a book. A moderate speed computer printer can print about 200 lines per minute. If one prime number were printed per line, how long would it take to print all those prime numbers? Express the answer in days, or years, whichever is more appropriate. If the printout has 60 numbers per sheet of paper, how thick would be the stack of sheets? If reproductions were made and sold at typical "textbook" prices, how much would a copy cost?
It would take 105 minutes = 69.44 days, and requires 3 × 105 sheets. A stack of 100 sheets of paper is about 1 cm thick. The total output would be about 3000 cm thick. This is over 1000 inches (1181, actually), or about 100 feet (98.4, actually). A 500 page textbook costs $60 in 1997. Therefore the 3 x 105 sheets would cost $36,000. Users of these tables are supplied a copy of the computer magnetic disk or tape, which is cheaper.
(A5) If we made a scale model of the earth the size of a bowling ball, how high would Mount Everest be on the model? The earth's radius is 6.4 x 106 meters; Mount Everest is 8.85 km high. Regulation bowling balls must not have a circumference greater than 27 inches. (Sports have not yet gone metric in this country.)
The circumference of the earth is 2πr. So taking ratio of height to circumference, h/27 in = (8.85×103 m)/[2×(6.4×106 m)]
h = 27×8.85×103/[2π×(6.4)×106] = 27(8.85)/[(2π)(6.4)]×10-3 inches
h = 5.94 × 10-3 inch.
That's 2.54 × 5.94 × 10-3 cm = 15.1 × 10-3 m = 1.51 × 10-2 m.
Our scale model of the earth the size of a bowling ball smoother than an actual bowling ball!
PROBLEM SET B
(Bl) The estimated amount of hydrogen in interstellar space is one atom per cubic centimeter. Our galaxy is shaped somewhat like a round disk, with a diameter of 300,000 light years and a thickness of 35,000 light years. Approximately how many atoms of interstellar hydrogen are there in our galaxy? (The data is only accurate to one significant figure, so express the answer accordingly.)
V = πr2h = 3.14 x (1.5 x 105)2 x (35 x 103) = 2.5 x 1015 cubic light years. 1 light year = 9.5 x 1017 cm, so 1 cubic light year = 8.6 x 1053 cm2. Multiplying by 7 x 1013 gives a result of 2 x 1069 atoms. This is still not as large as a duo!
(B2) 1000 grams mass of water at room temperature (20°C) has a volume of 1000 cubic centimeters. What is the mass of one cubic centimeter of water at this temperature? [Look this up in a reference book.] This is often taken to be approximately 1 gm/cm3. What percent discrepancy will result from use of the approximate value? Will this be significant in our work?.
At room temperature (20°C) the density of water is actually 0.99823 gm/cm3. The discrepancy is 1 - 0.99823 = 0.00177 or approximately 0.002 which is 0.2 %. This is not likely to be important in freshman physics lab!
(B3) Masses of atoms are measured using a unit called the unified atomic mass (u) defined so that the mass of the isotope 12C is exactly 12u. As a consequence, one u equals 1.660559 x 10-24 gm. The mass of an atom of iron is 55.934939 u. What is the mass of an iron atom expressed in grams? How many atoms are there in a gram of iron? Express both answers to 3 significant figures, using the rules of chapter 1.
Answer: (1.660559 x 10-27 kg/u)(55.934939 u) = 9.29 x 10- 26 kg = 9.29 x 10-23 gm. Insight is gained if we consider the units of the second factor to be u/atom. Then the result is kg/atom, a more complete description. This also helps in part two of the question, for we merely take the reciprocal of kg/atom to get atoms/kg. If the student doesn't discover this simple insight, point it out. The final answer is 1.076 x 1022 atoms/gm.
(B4) A flea can jump over a foot upward. If you could jump that well, relative to your size, how high could you jump?
From the table, the flea's size is about 1mm = 10-3 m. Let's say a person is 6 feet tall. Then h/(6 ft) = 1 ft/1 mm, or h = (6 ft)(1 ft)/(1 mm) = 6 ft (1 ft/mm) = (6 ft)(12 in/ft)(2.54 cm/in)(10 mm/cm) = 1828 ft. In miles it is 1828/5280 = 0.346 mile.
Easier: h = (1 ft)(1.8 meter)/(0.001 m) = 1800 ft.
That's over 500 meters high.
(B5) The theory of the moon according to the analytic methods of Charles Delaunay (1816-1872) contains one equation exceeding 170 pages in length. If the pages were the typical size of books of that era (9 x 6 inches), and laid side-by side in the hallway, how many feet long would the hallway have to be?
Answer: 170 × 0.5 ft = 85 ft.
PROBLEM SET C:
(C1) In the chart on page 3 of this experiment, the distance to the farthest known galaxy is shown. Check the consistency of this value with the value given in the footnote on page 3.
(C2) The unit of mass in the metric system was chosen so that the density of water would be 1 gm/cm3. The density of water changes slightly with temperature, but for most calculations this change is small enough to neglect. At room temperature (20°C) the density of water is actually 0.99823 gm/cm3. What percent discrepancy will result from using 1 gm/cm3 at this temperature instead of the more correct value? Will this be significant in our work? Calculate the correct volume (in cm3) of 1000 grams of water at 20°C.
At room temperature (20°C) the density of water is actually 0.99823 gm/cm3. The discrepancy is 1 - 0.99823 = 0.00177 or approximately 0.002 which is 0.2 %. This is not likely to be important in a freshman physics lab!
(C3) If you drew a "picture" of an atom one inch in diameter, how large would you have to draw the nucleus? Compare your conclusion with pictures of atoms you have seen in textbooks. Consider drawing a scale model of the solar system with the orbit of Pluto five inches in diameter. How large would the sun be on this picture? Compare with the pictures you have seen.
Nucleus size: 10-4 inches. Sun size: 5 x 10-3 inches. Textbook pictures are obviously exaggerated.
(C4) In elementary books, the atom is often described as a "miniature solar system." Consult the chart of page 3 of this experiment along with the results of problem C3 to determine whether this statement is an accurate analogy, at least with respect to the sizes of the components.
The atomic nucleus is smaller relative to atomic size than the sun is relative to the solar system size. It is about a factor of 10 smaller. Therefore the statement "atoms are mostly empty space" is essentially correct.
A related question which could be asked is: "What fraction of the atomic volume is occupied by its nucleus? Answer: 1/103 = 10-3.
(C5) The German philosopher Friedrich Wilhelm Nietzsche (1844-1900) said "The earth has a skin and that skin has diseases; one of its diseases is called man." Physicist Albert Abraham Michelson (1852-1931) told his students (at the University of Chicago) that mankind as a whole was rather insignificant on a universal view, merely "a skin disease upon the face of the earth." Consult the chart of sizes to determine whether this statement is an accurate comparison of relative sizes.
A 6 ft man is 1.8 meters high. But a better estimate of "average" size is about 1 meter. The earth's diameter is 12.76 x106 m. The size ratio, earth/man, is 12.76 x 106.
A microbe's size is about 2 x 10-8 meter. The size ratio, man/microbe, is 0.5 x 108 = 5 x 107.
It is a fairly good comparison, to within a factor of 10.
But should one compare linear dimensions? Why not compare the surface areas? Then the comparison would only be good to a factor of 100. See problem A6 for a comparison using the numbers of microbes on man and man on earth.
PROBLEM SET D:
(D1) Gerald Holton, Derek J. de Solla Price end others have estimated that "80 to 90 per cent of all scientists that have ever been, are alive now." Should this surprise anyone? How would this ratio compare with other professions? With the general population? Discuss, citing appropriate data from library research.
Comments:
Price discusses the growth of scientific activity in his book Science Since Babylon, in the chapter Diseases of Science.
In June 1989 the population of the world was nearly 6 billion. Other benchmark values (from various sources):

See Arthur H. Westling, "A Note on How Many Humans That Have Ever Lived." BioScience, July/August 1981. The "transition dates" in parentheses above are from this paper.
Doubling periods are indicated by square brackets above.
The total number of people who have ever lived has been estimated as 69 billion (through 1960). [See Keyfitz, N. "How many people have lived on the earth?" Demography 3:581-582 (1966).]
Westling improves the calculations, taking into account the change in average life span (from 20 years during early history to 50 in recent years). He concludes that 50 billion people have lived (through 1980). There were 4.4 billion people living on earth in 1980, about 9% of those who have ever lived.
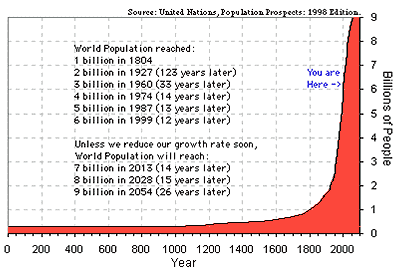
In 1997 the world population is estimated to be 5.8 billion (U. S. Census Bureau). This is growing at an estimated rate of 1.4% per year in 1996 (CIA World Factbook, 1996).
From "Ask Marilyn" by Marilyn vos Savant (Parade, May 26, 1991, page 26.): "As of last year, the world birthrate was about 27 per 1000 population, and the world death rate was about 10 per 1000 population. This translates to a growth rate of about 1.8 percent. Less-developed countries lead the pack, with a rate of 2.4 percent. And, at that rate, a population doubles in only 29 years."
A recent source gives the 105 billion as the number of people who have ever lived, and adds that 5.5% of all people ever born are alive today. [Haub, Carl. How many people have ever lived on Earth? Population Today, Vol 23, No. 2, (Feb 1995). 4-5 pp.] Every year new and supposedly better estimates of this number are published.
So, to say that 8 or 9 of every 10 scientists who have ever lived is alive today is indeed remarkable, for considerably less than 1 in 10 of all people who have ever lived are alive today. This shows that the rate of increase of scientists has been much greater than the growth of the general population.
Price concludes: "It must be recognized that the growth of science is something very much more active, much vaster in its problems, than any other sort of growth happening in the world today. ...science has been growing so rapidly that all else, by comparison, has been stationary."
(D2) Theodor Rosebury, in his fascinating book Life on Man (Viking Press 1969, Berkeley paperback 1970) estimates that the normal healthy skin of a person has about 1011 microbes. Estimate the total skin surface of a typical person and calculate the average number of microbes/cm2. How much area does each microbe have to itself, on the average? The human population of the earth is now over seven billion persons. How much land area does each person have, on the average? Make a meaningful comparison between the surface population of people on earth, and microbes on man. Don't merely compare the number/area ratios for the two cases, consider also the sizes of microbes and men.
Rosebury: A human being has an average of 5 x 106 bacteria per square cm of skin. The total skin area of a person is about 2 square meters. One student referenced the Encyclopedia Americana for a value of 1.7 × 104 cm2 of skin. That's 1.7 square meter.
Therefore, there are 1011 microbes on a person's skin. That's 2 x 10-7 cm2/microbe.
Information Please Almanac, 1974: The land area of the earth is 58,419 x 103 m2, and the population density is 63.4 persons/mi2.
[The entire area of the earth is 196,949,970 mi2. Only about 30% is land area.]
This gives 27.75 m2/person.
We'll use the linear size of the organism to estimate the surface area it occupies, as a basis for comparison.
A 6 ft tall man is 1.8 meters high. But a better measure of "average" size is about 1 meter. A microbe's size is about 2 x 10-8 meter.
The microbe size/area ratio: 2 x 10-8m / 2 x 10-7cm2 = 10-5 m-1.
Man's size/area ratio: (1 m)/(27.75 m2/person) = 1.86 x 10-5 m-1.
The comparison is very good!
(D3) (a) Find out the top speed of a garden snail moving across the ground in search of juicy leaves to munch on. (b) Express this in centimeters per second. (c) Express this also in the units furlongs/fortnight.
The garden snail is the fastest land snail, with a speed of 0.03 miles/hr. (An internet source gave it as 0.0313, but all these figures are unlikely to be significant.) Someone quoted the Guinness Book of World Records for a value 55 yards/hr; that's close to 0.03 mi/hr. We'll go with that.
Its speed is 1.34 cm/sec or 32 inches/minute or 53 yards/hr.
1 furlong = 1/8 mile = 220 yard.
1 fortnight = 14 days = 2 weeks.
(0.03 miles/hr)(8 furlong/mile)(24 hr/day)(14 day/fortnight) = 80.64 furlong/fortnight. 80 furlong/fortnight is good enough.
This document prepared in 1992, and revised in 2004.