Challenging Physics Problems.

Collected, edited and extended by Donald Simanek.

Textbook homework problems too often do not challenge student ingenuity and do not require the exercise of insight and creativity in their solution. Students can often solve them by plugging numbers into a textbook formula (or two) and grinding out an answer, the so-called "plug-and-chug" method.

It's good to occasionally tackle problems that can not be solved so easily, problems that challenge and frustrate. Here's a few examples. Most of these are old classics, a few are new.

1. Just rolling along.

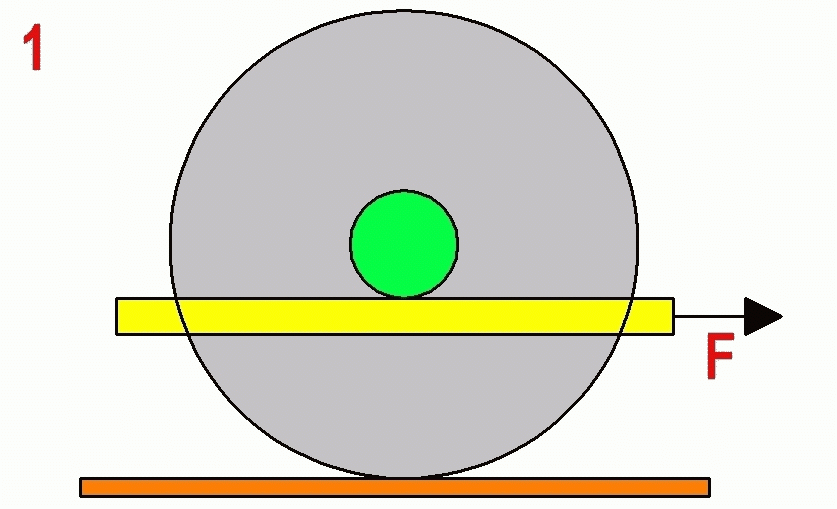1. Figure 1 shows a wheel (grey) with a central hub (green). It can roll freely on the flat, level tabletop. A beam (yellow) is pressed on the bottom of the hub and pulled to the right with force F. The radius of the large wheel is 13, the radius of the hub is 3. The beam, hub, and wheel all roll without slipping.

Which direction does the large wheel roll along the table?
How fast does it roll relative to the speed of the yellow beam?

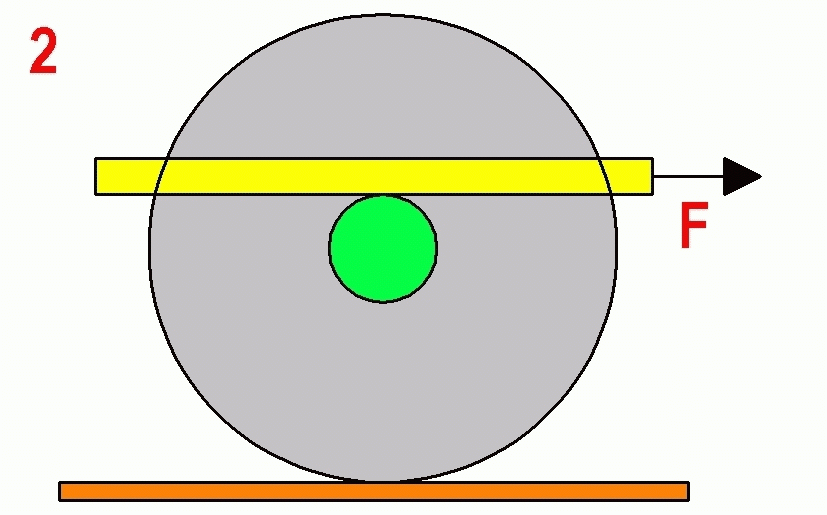2. Figure 2 shows a similar situation, but the beam rests on the top of the hub. Same questions.

3. Figure 3 shows another friction (or geared) roller contacting the hub. A beam rests on the top of it. Same questions.

Compare your answers. Are they at all surprising? Did you predict them correctly before you actually solved the problems?

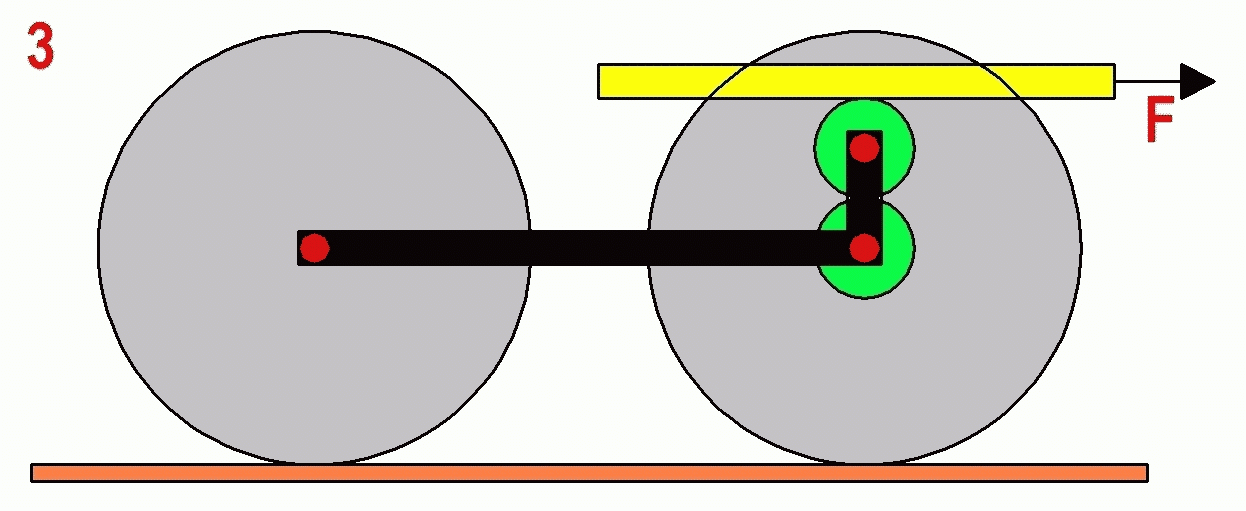4. Now, can you devise a mechanical cart that will travel opposite to the direction of the applied force, slower than the agent applying that force moves?

5. Can you devise a mechanical cart that will travel opposite to the direction of the applied force, faster than the agent applying that force moves?

Toys these days do not encourage this sort of inquisitive questioning and tinkering. One might argue that anyone who has ridden and repaired a bicycle would be familiar with this sort of mechanism. Or played with a yo-you toy. But most have not asked the questions and done the experiments to find the answers.

You can find mechanisms of similar type here: Directly downwind faster than the wind.

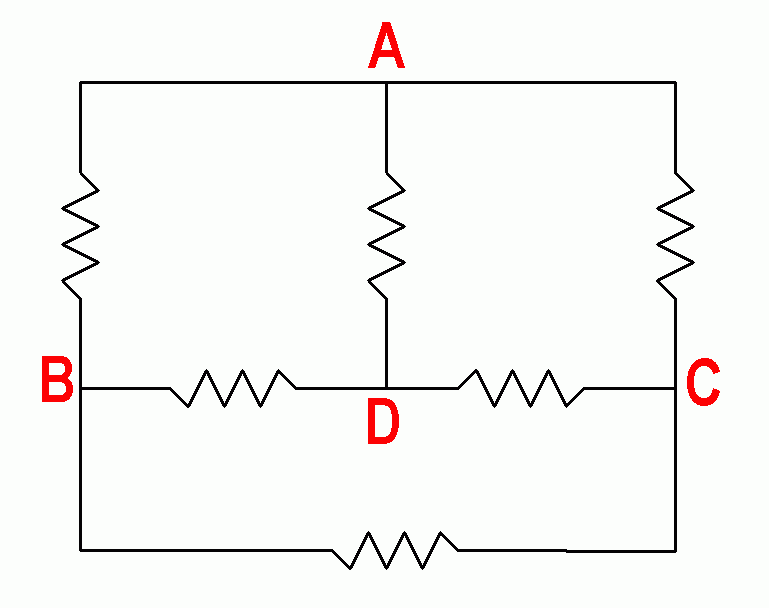2. The terrible
resistor tetrahedron.

This electrical network contains five equal resistors and one resistor that differs markedly from the others. How can you identify the different resistor by using only an ohm meter with the fewest measurements? What is the minimum necessary number of measurements in the worst case? In the best case (if you were lucky)? You may not disconnect or unsolder the resistors. You may not connect anything other than a standard ohm meter. Describe your method and reasoning. The four junctions are labeled for convenience.

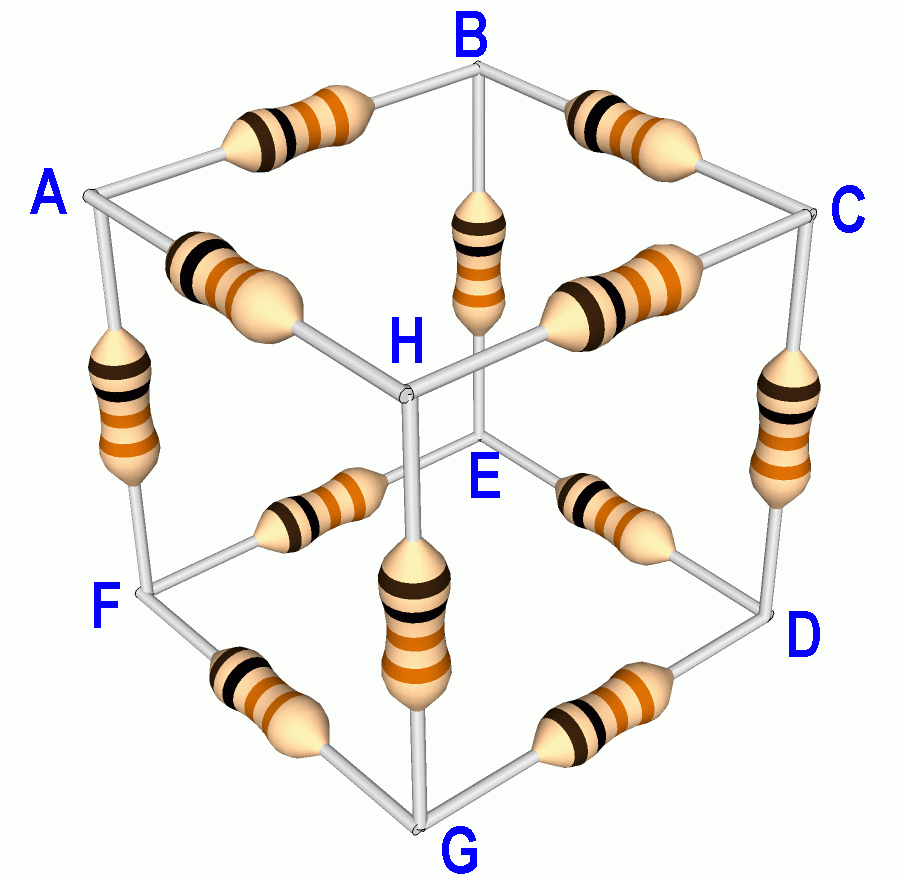3. The classic resistor cube.

This is an oldie, but still a goodie.

Twelve identical resistors of resistance r are soldered together in a cubic network.

(a) What is the resistance measured with an ohmmeter between A and C?

(b) What is the resistance between A and B?

Give all answers in terms of r.

Hint: This network has lots of symmetry. That allows for insightful solutions. There are also difficult solutions. See The Paleotechnologist for a difficult one, which is a good exercise in the use of the Wye-Delta transformations. That website is the source of the nice graphic. But you don't need all that. It's like using a sledgehammer to crack a walnut. Look for a simpler solution using Kirchoff's laws.

4. The classic resistor pyramid.

Solder six equal resistors of size r into the form of a equilateral pyramid. The result will be a network just like that shown flattened in problem 2 above. What is the resistance of the pyramid between any two junctions in terms of r?

5. Where on Earth?

Where on the surface of the earth could you travel 1 mile south, 1 mile east and one mile north and end up at your starting point?

One answer is easy to find. But there are other answers. Many of them. Where are they and how many are there?

6. Walking the dog.

Jane is walking her dog, spot. She sees her friend, Dick, walking toward her along the same long, straight road. Both Dick and Jane are walking at 3 mph. When Dick and Jane are 600 feet apart, Spot runs from Dick to Jane, turns and runs back to Dick, and then back and forth between them at constant speed of 8 mph. Dick and Jane both continue walking toward each other at a constant 3 mph. Neglecting the time lost each time Spot reverses direction, how far has Spot run in the time it takes Dick and Jane to meet?

Answers and discussion.

Return to Donald Simanek's page.
Return to the top of this document.
Return to The Museum of Unworkable Devices' Main Gallery.