A Descriptive Explanation of Ocean Tides.

This documenet has been significantly revised Nov. 2022. Suggestions are welcome.

Fig 1. The moon and sun create tides and drive their regularity..

Anyone who has spent some time on a beach has noticed the periodic phenomenon of the ocean tides. The water level at the shoreline rises to a maximum, then the tide goes out, but it rises again about 12 hours and 25 minutes later. This process is synchronized to the moon's apparent motion in the sky, with period 24 hours and 50 minutes. We also observe smaller tides that are synchronized with the motion of the sun in the sky. Water levels at shorelines vary considerably in size and arrival time at different places on earth, resulting from variations in shoreline topography. There are significant large variations of water level throughout the oceans, due to reflection of water from shorelines and resonant phenomena of water sloshing in the confines of an ocean basin. [1] Yet the relentless time-regularity of tides, observed since the earliest history of mankind, is clearly driven by the positions of the moon and sun relative to our location on earth.

Ancient man considered the tides an occult or magical influence of these heavenly bodies. Now that we recognize that all motions of planets and their satellites are due to the universal gravitational force, we can better understand this connection in detail, removing its mystery.

Not only does gravity rule the motions of the planets and moons, but gravitational forces also stress material bodies, causing distortions of their shape. Those distortions are relatively small in magnitude, but they represent a considerable expenditure of energy over the huge mass of a body like the earth. For example, the average radial distortion of the earth's "solid" crust due to the moon's gravity is about 20 cm, and the mid-ocean water level is raised to an additional one meter in height. But the amount of water volume that must shift to achieve that height in the Atlantic or Pacific Ocean is huge. We call these land and water distortions "tidal bulges". [2] As the earth rotates underneath the ocean's tidal bulges, the water acts much like the water in a dishpan as you try to carry it. The water "sloshes around" bumping against the container walls, setting up standing waves. This is why ocean shoreline tides can be of much greater amplitude than the average size of the tidal bulge itself. It is also the reason that the timing of arrival of coastal high tides can be many hours "late" in arrival at places such as the North Sea, and why tides in the Mediterranean sea are so small in amplitude, and why there's only one lunar tide per day on parts of the shoreline of the Gulf of Mexico.

The tides synchronized with the moon are the largest, about 2.2 times greater than the tides due to the sun, so we will confine our attention to them. Tides synchronized with the sun are caused by the same gravitational mechanisms.

Why is there usually a high tide when the moon is high in the sky, and also when the moon is on the opposite side of the earth? One often sees "explanations" that speak of "the moon pulling on the water". It's not that simple. The moon's gravitational force on earth acts on all parts of the earth with nearly the same force, differing by only about 7% on the sides of earth nearest and farthest from the moon. The differences from ocean surface to the ocean floor are far smaller. But it's those small force differences that are responsible for the tidal force or tide-raising force that distorts the earth's shape and the bodies of water on it. These forces raise two tidal bulges on opposite sides of the earth. Though these are relatively small, rasising ocean water levels only about 1 meter, they are of large extent and we will see that they are the driving force for periodic tides all over the earth.

The processes that shape the earth are linearly additive and may be considered one at a time.

The shape of the earth.

1. The gravitational field of the earth.
2. The rotation of the earth on its axis.
3. The gravitional fields of the moon and sun.
4. The presence of continents, and ocean floor and shoreline topography.

1. We start with an earth that does not spin, and has no outside influences (like the moon). Earth's gravity makes the earth go round. When the earth was molten it shaped the earth into a sphere. If the earth is covered entirely with an ocean, that ocean has a spherical surface. We must not include earth's gravity in subsequent steps. We are done with it.
2. Now add earth's axial spin. This results in the equatorial bulge and polar flattening. We must not consider axial spin as a cause of earth and water deformation in subsequent steps.
3. Add a satellite (like the moon). We consider the effects of its gravitational attraction on earth, and only these. The moon's gravitational forces are the sole reason for the tidal bulges. It is the small divergence of moon's gravitational field lines and the inverse square law of the strength of the moon's gravitational field that causes stretching and compressing of earth's solid materials and "pushing" of its ocean waters.
4. Add continents that distort and amplify ocean and shoreline tides due to seafloor and shoreline topography. Detailed analysis of this is beyond the scope of this paper.

The source of tidal bulges.

One way to get a feeling for the size and direction of tidal forces is to use vector algebra to calculate the size and direction of the difference between these forces acting on opposite sides of a chunk of solid matter at the surface of the earth. The following diagram shows this for several points on the surface of the earth.

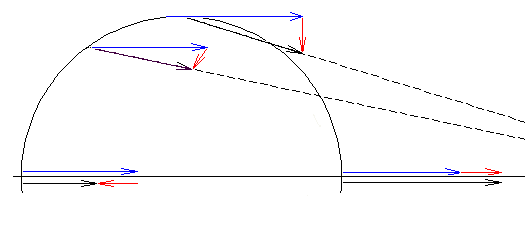Fig 2. Vector analysis of tidal forces. The moon is to the right. The dotted lines converge to it. It is drawn very close to the earth, so that the vector diagrams will be easier to interpret. Blue vectors are the average forces due to the moon's gravitational forces. These are all equal and parallel. Black vectors are gravitational forces due to the moon. Red vectors are the differences between the gravitational force and the average force. These are the tidal forces.

Note that on the side of earth facing the moon, the tidal force along the earth-moon line points toward the moon. On the side of earth opposite the moon, the tidal force along the earth-moon line points away from the moon. This is because on the lunar side the moon's gravitational force is greater than average. On the far side it is less than average.

This diagram shows that the forces on a solid body stretch chunks of solid material in one direction and compress them in the perpendicular direction. [This is more properly called the "force gradient" over the volume, a concept from calculus.] We can make a map of these stress "forces" over the surface of the earth and it looks like this: [3]

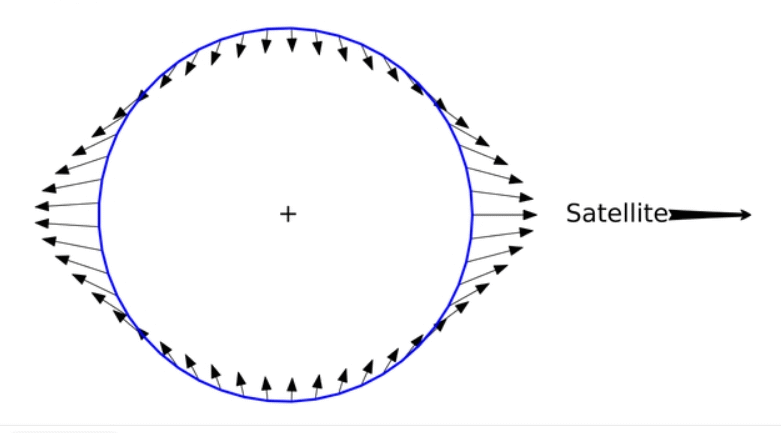Fig 3. Tidal forces due to a satellite of earth (the moon). From the Wikipedia. The relative sizes of forces are exaggerated for clarity.

The vectors in this diagram can be thought of as differences between the gravitational force on chunks of matter and the gravitational force averaged over the entire earth. They are departures from the average force. [4]

These forces act on the earth's volume in two ways: (1) They stretch the "solid" earth along the earth-moon line, and (2) they move materials, especially fluid materials like water, toward the earth-moon line. The second effect is dominant for ocean water, since water is nearly incompressible. It does not compress or stretch, but it is easily pushed around. The tidal forces push water toward the tidal bulges. Outside of the bulge the ocean surface is lowered.

This displacement of water contributes to two tidal bulges on opposite sides of the earth. This is the reason for the tidal bulges in oceans, and it is these bulges that drive the periodicity of the shoreline tides that we observe while basking on the beach, as the earth turns on its axis underneath these tidal bulges.

If you draw a smooth curve connecting the vector arrowheads in Fig 3 you will have a greatly exagerated picture of the shape of the distorted earth. It shows the tidal bulges and also the depression extending around the earth at 90° to the earth-moon line.

Size matters.

Water in a tidal bulge must come from somewhere. In a large body of water such as an ocean, water moving into a tidal bulge must be accompanied by water levels lowering outside of the bulge. So tidal bulges can only form in bodies of water of large area. Bulges are much smaller, nearly insignificant, in lakes. In smaller bodies of water, like your backyard swimming pool, the water does not have enough extent in area to form perceptible tides. Look again at the diagram of tidal forces and note that there must be some inward directed tidal forces outside of the bulge area. In small bodies of water there's no source of water to contribute to a tidal bulge.

The tidal forces on ocean water have two componenets, a radial component along an earth radius and a tractive (pulling or pushing) component tangent to the earth's surface. It is the tractive components that push water toward the tidal bulges.

Fig. 4. How the tractive components of tidal forces push water toward a tidal bulge, as seen from above the center of a bulge (designated by +).

If this is difficult to visualize, compare a pan partly filled with water. Move it back and forth to set up a standing wave. Water lifts in height in one part of the pan when it lowers in height in another part of the pan. If there are corks floating on the water, they all move up and down and only slightly sidewise back and forth, but none rush all the way from positions of lowering water to positions of rising water. The same would be true of pebbles on the bottom of the pan. Fish in the ocean need not fear being swept from Alaska to Hawaii and back in half a lunar month as tidal bulges rise and fall, which would be terribly destructive to ocean life.

While gravitational forces depend on the inverse square of distance, these tidal forces, being differences in force over length (ΔF/Δx), depend on the inverse cube of distance. That's why tidal forces on earth due to the sun are much smaller than those due to the moon. Even though the sun's mass is very much greater than the moon's mass its distance from earth is much greater than the moon's distance. [The reader may wish to do a "back of the envelope" calculation here.]

There's an interesting confirmation of the importance of water's incompressibility and the availability of enough water to contribute to a tidal bulge. It is observed that the level of water in stone wells decreases when the moon is highest overhead. The land tide stretches the solid walls of the well, increaseing its volume, but the water in the well maintains its original volume. Remember that water is incompressible. So the surface level of a constant volume of water in a well that increases in size (volume and height) will lower, measured with respect to the walls of the well.

Rotation is not an issue.

Lunar gravitational forces alone are responsible for the tidal forces. Some textbooks confuse the matter by talking about "effects due to rotation" or due to "inertia" or "centrifugal force". [5] Rotation of the earth on its axis does indeed cause an "equatorial" bulge of land and sea, extending entirely around the earth. This is quite different from lunar and solar induced tides. For one thing, the equatorial bulge is constant in shape over time, axially symmetric and not in any way related to the position of the moon or sun. The lunar tides are a small additional distortion added to that equatorial bulge, and they are relatively fixed in position relative to the moon, not to the earth. [For more about this, go to Appendix: The centripetal seduction.]

One effect of rotation does matter—a lot. If the rotating earth had no continents, oceans would still experience frictional drag with the ocean floor, and their tidal bulges would be displaced about 3° from the earth-moon line. Since the earth rotates on its axis faster than the moon revolves around the earth, the tidal bulges are dragged ahead of the earth-moon line. So high tide occurs later than when the moon crosses the observer's meridian.

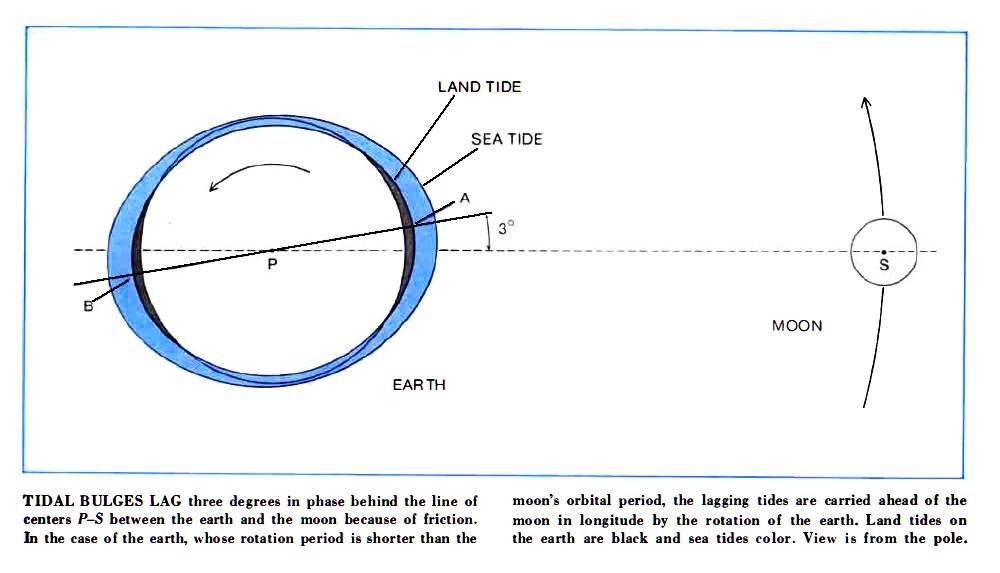Fig 5. The diagram shows the tidal bulges accurately but the size of the bulges is exaggerated and the moon is shown close, for clarity. The moon is actually much farther away. The earth rotates counterclockwise faster than the tidal bulge and the moon, so we experience high tide later than when the moon is highest in the sky. © Scientific American.

Complications.

Wandering moon.

Endnotes.

[2] Ocean tidal bulges are not directly observed or measured. They are part of a model, based on well known physical laws, to account for the observed tides that are measured, primarily at shorelines. Land tides may be directly measured.

[3] This is done more rigorously using calculus. But looking at this map as a picture of departures from the average force is conceptually correct. Notice that these vectors sum to zero when summed over earth's surface and also when summed over the entire volume of earth.

[4] A similar map would result if we just took the difference between the net force on a mass at the earth's surface and the force on the same size mass at the center of the earth. This, however, seems to relate two things that are very distant from one another, which can be misleading.

[5] Inertia is just another name for "mass". If someone uses inertia in an explanation, ask them what units are used to measure inertia. Lord Kelvin's advice is still a good rule: "When you can measure what you are speaking about, and express it in numbers, you know something about it. When you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind. It may be the beginning of knowledge, but you have scarely, in your thoughts, advanced to the stage of science.”

Centrifugal force has several meanings. None of them cause or contribute to tides.

Centrifugal force is a fictitious force, a convenience trick only appropriate when doing problems in rotating reference frames, which are non-inertial frames of reference. It is convenient for mathemataical calculations, but we do not use it here, for we are using an inertial reference frame. But even when fictitious forces are used appropriately in a rotating reference frame, it turns out that the centrifugal force is constant in size and direction over the entire earth, and therefore cannot raise a tide. To nail its coffin even more securely, fictitious forces are merely computational aids and cannot introduce new physical effects into the physical processes being analyzed.

In inertial frames centrifugal force is sometimes defined as a force equal and opposite to the centripetal force, where centripetal force is nothing more than a label naming the radial component of the net force on an object moving in a circular path. This was already disposed of as the cause of the equatorial bulge, which is symmetric about the rotation axis of the earth. Tides are not axially symmetric.

Many elementary treatments in textbooks and websites invoke centrifugal force without even specifying what sort of reference frame is assumed. Beware of these, or any that invoke centrifugal force in any way as an "explanation", for tidal forces are incorrect and misleading, leading only to confusion, not enlightenment.

[6] Even the best textbook diagrams often explicitly show and label the rotation axis of the earth and the North geographic pole, and show the moon's orbit on the equatorial plane. Actually the moon's orbital plane is tilted 5.15° with respect to the earth's equator. The earth's axis is tilted 23.5° to the ecliptic. This produces a complicated variation of the tidal bulges over time, north and south of the earth's equator. It is best to ignore the North pole if it is shown in the diagram. By convention, diagrams of the solar system are shown looking down on the north polar region of the earth.

Thanks to Fred Bucheit for perceptive and useful suggestions for the improvement of this document.

Web sites worth a look.

Listing a link here does not imply total endoresement of everything found there, nor of anything by the same author on other subjects. But that should go without saying.

1. Butikov, Eugene. A dynamical picture of the oceanic tides. Am. J. Phys., v. 70, No 10 (October 2002) pp. 1001-1011. We have treated only the case of tides on a spherically symmetric earth, either an earth with no continents (covered with water), or a solid earth with no oceans. Once you include oceans and continents, resonance effects occur in ocean basins. This can be complex. Dr. Butikov's paper is an excellent treatment.

2. Butikov, Eugene. A set of Java-applets that are beautiful dynamical illustrations of the tide-generating forces and for the wave with two bulges that these forces produce in the ocean. [Some browsers, including Chrome, do not support Java. See Sirtoli's paper for equivalent animations.]

3. Butikov, Eugene. Oceanic Tides: a Physical Explanation and Modeling. Computer tools in education, 2017 No. 5: 12–34. A somewhat simpler treatment of the subject of the previous paper.

4. Butikov, Eugene. The Physics of the Oceanic Tides. A further development of the approach of Butikov's 2002 paper.

5. Denker, John. Tides. A treatment of tides with a personal style and viewpoint, not just an echo of standard treatments.

6. Hicks, Steacy Dopp. Understanding Tides. A comprehensive and readable treatise on tides.

7. Johnson, C. Mathematical Explanation of Tides. This treatment is more complete than mine. I would choose to express some things differently, but it makes the same important points as my document: (1) you don't need to talk about centrifugal force or use a rotating coordinate system to understand the tides, and (2) many textbook treatments are misleading or wrong.

8. Kluge, Steve. A Brief Explanation of Varying Range and Height of Tides. Many textbooks mention that some places on earth experience only one tide per day, but few take the trouble to explain why. This website does.

9. NOAA (No author given.) Our Restless Tides. A standard treatment. The author is not always clear about the frame of reference being used, but this still has some good information.

10. Sawicki, Mikolaj. Myths about Gravity and Tides. The Physics Teacher, 37, October 1999, pp. 438-441. This article discusses a wide range of misconceptions about the tides.

11. Sirtoli, Paolo. Tides and centrifugal force. This document has some excellent animations that make it all very clear. Sirtoli says that he was "inspired" by my treatment of tides, but he has done a far more comprehensive treatment (including the mathematics and animated diagrams) than I have. He shows why centrifugal effects are not the cause of the tidal bulges.

12. A good, fast paced video, What Physics Teachers Get Wrong About Tides! A correct explanation of the reasons for tidal bulges.

13. Web sites and textbooks are often wrong in their explanations of tides, promoting mistakes and misconceptions. These are exposed and discussed in Tidal Misconceptions.

14. A web search for "ocean tides" turns up both good and bad web accounts, many having mistakes and misconceptions. But search for 'tidal forces' and you find better web accounts, including that in the Wikipedia: Tidal Force.

Appendix: The centrifugal seduction.

These two figures (Figs. 6 and 7) should dissuade anyone from such futile efforts. Fig. 6 shows the result of earth's rotation about its axis (black line). The distortion (equatorial bulge and polar flattening) is symmetric about the axis. Fig. 7 shows the result of the slightly divergent gravitational field of the moon. The earth/moon line is shown in black. The distortion is symmetric about that line.

For a tactile model of tidal bulges, consider an egg. The bulges of the egg are exaggerated, and also asymmetric, compared to the earth, but you can ignore that. Imagine an axis along the symmetry axis of the egg that represents the earth-moon line. Or use a boiled, peeled egg and thrust a long wire through its axis. The egg does not rotate about this axis. Now, ask yourself where in this model there's any shape distortion of the egg that would be caused by centrifugal force.

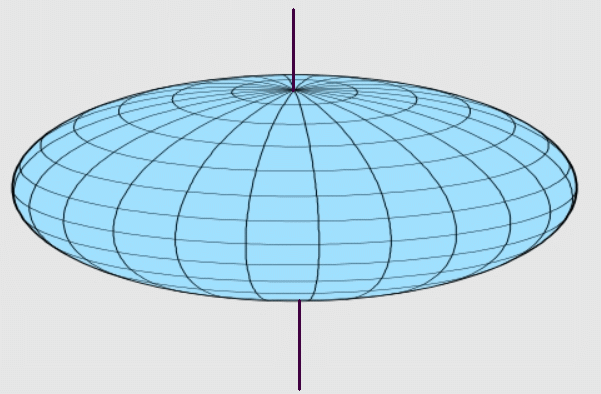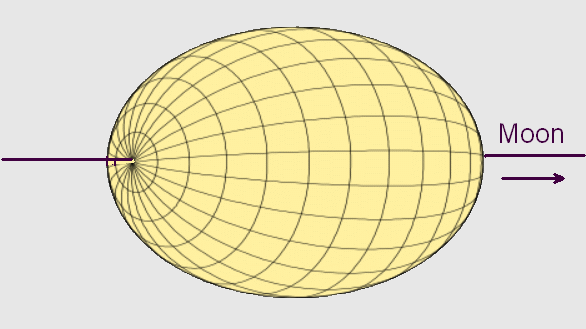Fig. 6. Distortion of earth due to its rotation. From the Wikipedia.	Fig. 7. Distortion of earth due to the moon's gravitation. From the Wikipedia.

These figures are intended to show the 3d appearance of these ellipsoids of revolution. The grid lines of Fig. 6 are latitude and longitude lines. The vertical line is the rotation axis of the earth. The grid lines of Fig 7 are not longitude and latitude lines. They are only to suggest the 3d shape of the earth. The distortions are exaggerated, for the actual distortions are such a small effect that the earth would still appear spherical on this scale.

Textbook illustrations seldom show these effects in 3d, but only show flat cross sections. This may be the reason why so many are seduced into supposing that Fig. 7 shows the effect of centrifugal forces.

Whether you analyze tidal bulges in an inertial or non-inertial reference frame, centrifugal force plays no role in creating or sustaining the bulges.

Text © 2011, 2003, 2015, 2017, 2020, 2022 by Donald E. Simanek. Input and suggestions are welcome at the address shown to the right. When commenting on a specific document, please reference it by name or content.

Latest edit: 2022.

Return to Tidal Misconceptions.
Return to Donald Simanek's home page.