Inelastic Collisions.

Example 1. Two balls of sticky putty collide.

Consider two equal mass balls of size m made of sticky putty. One is at rest. One moves toward the other at speed v. They collide and stick together. The combined mass (2m) moves away at speed v'. Draw the picture before and after collision. The conservation of momentum equation is:

[1]

    mv = (2m)v'

From which we conclude that v' = v/2.

So the final speed of the combined putty blob is half the initial speed of the moving ball of putty, v' = v/2. What about the conservation of kinetic energy?

[2]

    (1/2)mv2 = (1/2)(2m)(v')2 + Thermal energy

[3]

    (1/2)mv2 = (1/2)(2m)(v/2)2 + Thermal energy

[4]

    (1/2)mv2 - m(v2/4) = Thermal energy

[5]

    mv2/4 = Thermal energy

So half of the initial kinetic energy goes into thermal energy, heating the putty.

Example 2. Perfectly elastic collision between equal masses.

We now consider a special, but interesting, case. Two equal masss balls of mass m collide. One is initially moving with speed v1. The other one is initially at rest. After the collision we cannot claim to know the sizes or directions of the velocities, but we will call them v1' and v2'. Draw the situation before and after collision, assuming that the moving ball is initially to the left of the stationary ball, and the moving ball has speed v1 to the right.

Let's assume that these balls are so elastic that no thermal energy is produced in the collision.

The conservation of momentum and conservation of energy equations may be written.

[7]

    m1v1 = m1v'1 + m2v'2

[8]

    (1/2)m1v12 = (1/2)m1(v'1)2 + (1/2)m2(v'2)2

But in our case m1 = m2, which simplifies these equations to:

[9]

    v1 = v'1 + v'2

[10]

    (v1)2 = (v'1)2 + (v'2)2

Square equation 9.

[11]

    (v1)2 = (v'1)2 + (v'2)2 + 2v1v2

Combine equations 10 and 11 to eliminate v1. The squared terms all drop out.

[12]

    0 = 2v1v2

This has two solutions, since it came from a quadratic equation.

Solution 1: When v'2 = 0, then v'1 = v1. This corresponds to the uninteresting case when the balls actually don't touch, perhaps because the first ball was aimed badly.

Solution 2: When v'1 = 0, then v'2 = v1. This says that the first ball stops dead and the second (initially unmoving) ball moves away with the same speed the first ball had.

This is the result observed in the actual collision between two very elastic balls, say balls made of steel, brass, hard wood, ivory, hard plastic, or even those "high bounce" toy "superballs". This is the only result that occurs. One might think, if one only considered conservation of momentum, such a result as this might occur: Ball 1, initially moving with speed v might have speed v/4 and ball would have speed 3v/4. That would satisfy conservation of momentum, and many other outcomes could be envisioned that would also satisfy conservation of momentum. But once we insist that we also must satisfy conservation of kinetic energy, then only one result comes from this collision, the one described in Solution 2.

The problem becomes more interesting when we have three or more identical elastic balls in a row, initially touching. This is the toy called the Newton's cradle which usually has five balls. (Actually Newton didn't invent it.) Though the toy is fun to play with, its analysis is beyond the level of this course. Why? Because additional constraints, beyond simply conservation of energy and momentum, apply to the collisions, due to elastic compression, and the finite velocity of compression pulses through the body of the balls.

Collisions in two dimensions.

Here's a nice problem set to test your understanding of energy, momentum, and vector mathematics.

1. Two identical perfectly elastic hockey pucks are on a frictionless, level surface. One is initially at rest. The other moves toward it with speed V, without rotation. They collide and both have different velocities after collision. Prove that their velocities after collision are at a right angle to each other, no matter what the impact parameter.

2. Could the pucks ever have the equal velocities after collision? Under what conditions?

3. Could one of the pucks have zero velocity after collision? Under what conditions?

4. Why does the above 90° angle outcome not happen in one special case, and what is that case?

5. Why can we be certain that under these conditions the pucks will not be rotating after the collision?

Clearly we will need to use a two dimensional coordinate system to solve this problem. Here's a picture of the situation.

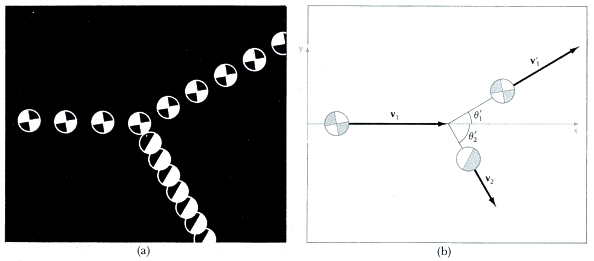
(a) is a photograph of the collision seen from a camera above, using strobe photography. The pucks are on an air suspension table, which gives nearly frictionless support for the pucks on a cuscion of air. The pucks have different designs on their upper surface to distinguish them and also the reveal any rotation they might have. Here they have no rotation. The spacing between images reveals their speeds, which could be calculated if we know the flash rate of the strobe light.

(b) shows this in an xy coordinate system. We must show that whatever the impact parameter, the emergent angles of the pucks add to 90°.

Puck (1) is coming from the left. Puck (2) was initially at rest.

The impact parameter is the distance of the stationary puck (2) from the line of action (straight line path) of the moving puck (1). It turns out that we will not need the value of this to answer the limited questions posed here.

Since there's no puck rotation before or after collision, we will not need the conservation of momentum equation to answer the first four questions.

Diagram (b) suggests that we might use Cartesian coordinates and trigonometry to solve tis problem. But there's an easier way.

The pucks are identical. Let their mass be M.

The conservation of energy tells us:

[13]
(1/2)MV12 = (1/2)Mv'12 + (1/2)Mv'22

The conservation of momentum equation is:

[14]
MV1 = Mv'1 + Mv'2

In both equations we can drop out the common factors (1/2) and M, leaving

[15]
V12 = v'12 + v'22

and

[16]
V1 = v'1 + v'2.

Now, remember the Pythagorean theorem. It says that the sum of the squares of the lengths of two legs of a right triangle is equal to the square of the length of the hypotenuse. And a right triangle is the only triangle for which this relation is true. The vector polygon of the equation [15] is a triangle. Equation [14] tells us that the sum of squares of the lengths of two sides of this triangle add to the square of the third side. So that's exactly what we have here, a aright triangle. Make a drawing for yourself. Therefore we conclude that the angle between v'1 and v'2 is 90°.

Could the pucks ever have equal velocities after collision? No.

Could one of the pucks have zero velocity after collision? Yes, in two cases. (1) when the collision is head on (the impact parameter is zero) puck 1 comes to rest and puck 2 moves with velocity V exactly along the same line, conserving energy and momentum. (2) When the collision is just grazing the edge of puck 2.

What is the exeption to the 90° outcome? It may seem that the two exceptions are the two mentioned in the previous paragraph. But in vector analysis, two vectors are defined to be perpendicular when their dot product is zero. That applies to these two cases, where one velocity is zero.

Why don't the pucks ever rotate after collision? You might think that sometimes they might both rotate after collision, one clockwise, one counter clockwise, at the same angular speed, thereby conserving angular momentum. This would require that each puck experienced a torque at collision. But in this idealized case, at collision the forces on the pucks are along the line joining their centers. So these forces exert zero torques on the pucks.

This is also the reason that puck 2 moves away along the line through the puck centers at impact.

Go to the next chapter, Ball bouncing from a massive wall. A surprising and instructive example.
Return to the contents page of A Brief Course in Classical Mechanics.
Return to Donald Simanek's front page.