Physics Lecture Demonstrations,
with some problems and puzzles, too.
Compiled and annotated by Donald Simanek
The internet has many sources of lecture demonstrations, particularly of demos suitable for large lecture courses. I list just a few.
- Physics demonstrations, Science Exhibits (Bill B's Homepages)
- Julien C. Sprott, University of Wisconsin. Descriptions, safety and presentation hints, data, literature references. A very rich and useful collection of physics demonstrations.
- University of California at Berkeley. Nice drawings of entire setups.
- University of Minnesota. Color photos.
- Boston University. Line drawings.
-
Jeff Whittaker's Physics Lessons. Resources for physics teachers. Especially, see
Physics Demos. Brief descriptions with whimsical pictures, some animated. This is useful catalog of ideas for someone who already has familiarity with physics demos. Usually no explanations are given, nor any hints about how to make the demo most effective in a classroom situation.
Often the university sites exist primarily for internal use, listing equipment and demos available to physics professors teaching large sections of introductory courses. They usually give lists of required equipment, they don't always give much information about setup, effective presentation and explanation of the physics.
In my little collection of demos I have included many that are appropriate for smaller classes and classrooms. I consider these demonstrations particularly well-suited for integration into a lecture/discussion in an informal setting.
I'm in the process of improving and refining this document, and intend to include more illustrations, discussion of the underlying physics, and presentation suggestions. Keep watching this space.
How and why to present demonstrations
Over the years since Newton, physics teachers have developed a vast catalog of physics lecture demonstrations, which fill many books.Too often these demo books merely describe the demonstration, but don't explain the physics behind it, nor suggest effective ways to present it. Too often teachers use these demonstrations primarily for entertainment in physics classes. My own philosophy on the use and misuse of demos is reflected in these questions you should ask before doing a demo.
- Does the demonstration fit into the story line of your lectures?
- Is the demonstration important enough to justify building a story line around it?
- Does the demonstration clearly illustrate a phenomenon, principle or law of physics? If too many interacting principles affect the outcome you might consider selecting a "cleaner" demo.
- Can the physics of the demonstration be understood at the level of the course? If not, don't do it.
- Do you, the presenter, understand the demonstration fully? If not, don't do it.
- Ask yourself whether you do the demonstration for entertainment, or because the physics behind it needs this kind of reinforcement.
To do a demonstration without explanation and discussion is pointless. You should:
- Practice the demonstration until you have it perfected. Present it to a critical observer you can trust to tell you what's wrong with it, what points are not clear, and what details of explanation you've omitted.
- Be sure you know what the demonstration demonstrates—not what you intend it to demonstrate, but what the students see in it, and what they think about what they see. I.e., find out what it demonstrates to them and what they actually get out of it.
- Prepare the students for the demonstration. Show the apparatus, describe what you intend to do before you do it. Tell your audience what the demonstration will teach us about physics, or what part of physics it will put to the test. Suggest what the audience should watch for.
- Ask students to predict in advance what will happen. Do not proceed until at least some students have provided good physical reasoning for their predictions.
- When you have made the experimental situation clear to everyone, and have their attention, do the demonstration.
- Analyze the demo. If some predictions were wrong, find out why. Do the demonstration again during the discussion.
- Be prepared to test hypotheses raised by students by doing a modification or variation of the demonstration, and making some measurements.
What does it demonstrate?
The staged bit of physics we call a demonstration is done to illustrate and reveal a physical process or principle. Are we sure what principles are being demonstrated? If not, we should rethink the matter.
The bottom line is what is demonstrated to the students, that is, "What do students see in it, and what do they understand about it?" Often that isn't what we intended. If students take concepts away from a demo that are incomplete, wrong, or misleading, our purpose has been thwarted.
Consider the classic tablecloth pull and its variants, often passed off as demonstrations of inertia. To say that objects on the table remain in place when the tablecloth is yanked from under them is because of their inertia isn't entirely wrong. But it isn't the whole story, and isn't helpful to understand the outcome of this experiment. The audience didn't see anything that showed that objects with different inertia (mass) behaved differently. I consider these to be primarily demonstrations of impulse. They show that in a situation where the size of a force is essentially independent of the time it is applied, then the impulse of that force can be made very small by reducing the time during which it is applied.
Another so-called "inertia demonstration" is that of the heavy ball suspended by a string with another string dangling. (See my discussion below, titled jerk.) Inertia of the heavy ball plays an important role here, but one doesn't understand the demo until one considers the mechanism of how string breaks and the fact that the string must be physically stretched before it breaks. One must analyze the tensions that cause the stretch. The fact that a steady pull causes the upper string to break is easy enough to grasp, for its tension is greater than the lower one by amount equal to the weight of the heavy ball. This part of the demo has little to do with inertia. But when the lower string is jerked, why does its tension increase to the breaking point before the upper string? Here's where the inertia of the ball is important. The tension on the lower string increases to the breaking point in so short a time that the ball hasn't moved far enough to stretch the upper string enough to break it. Unless these points are brought out, the demonstration is little more than a gee-whiz bit of stage magic.
One more example, from Martin Gardner's The Last Recreations,
Springer-Verlag, 1997. (Used with Mr. Gardner's permission.)
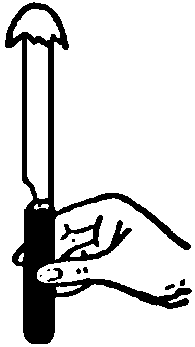
Inertia is the secret behind the following bet. Get a kitchen knife with a sharp point, hold it vertically, and hang half an eggshell over the point [as shown in the figure]. Challenge someone to puncture the shell by rapping the knife handle on a table or kitchen counter. Each time one tries, the shell bounces off the tip of the knife unharmed. But you, who understand physics, can crack it at will. The secret is to hold the blade loosely in your hand. Make this appear as if you rap the handle on the counter when in fact you allow the knife to fall by its own weight so that it hits the counter and bounces. The imperceptible bounce sends the knife point through the shell.
I can just hear Robert Ehrlich and Cliff Swartz groaning, complaining that this isn't a demo, it's a deception, and such deceptive tricks are best avoided in a physics class.
Does this "demonstrate" inertia? Inertia does play a role here (doesn't it play a role in almost everything?) But there's more physics to this demo than that. If a you want to bring out all of the physics in this demo, you need to discuss these details:
- The person trying to forcefully rap the knife on the table will cause the knife to move downward faster than free-fall, therefore when the knife hits, it won't be in contact with the eggshell. The motion of the knife is damped by the hand holding it and is over by the time the eggshell drops onto the stationary knife-point. That impact isn't forceful enough to break the shell. The small inertia (mass) of the eggshell plays a role here.
- But when the knife and eggshell are allowed to fall freely they remain nearly in contact because their accelerations are the same. There may be some aerodynamic drag on the inverted eggshell, but not enough to cause the shell and knife to separate much, and a little separation doesn't matter.
- The knife bouncing on a hard (elastic) table-top rebounds upward with nearly the same speed it had when it hit the table. Therefore the relative speed of knife point and egg shell is roughly twice what it would be if you held onto the knife and forcefully hit it against the table. This is enough to puncture the eggshell.
Oh, yes, I almost forgot. What principle of inertia was demonstrated in this experiment? Seems rather trivial, doesn't it, now that we've analyzed the real physics secrets behind this experiment.
Showmanship tips
I have seen many shoddy presentations of physics demonstrations. Teachers should seek out members of the speech and drama department to critique their performances. Professional, or even amateur, magicians can give invaluable advice on how to communicate one's intentions to an audience (and hide one's deceptions, but that's not a skill you'll need in physics).
Use apparatus large enough for the audience to see clearly. Consider super-sizing it.
If something can be seen only in a narrow range of angles, stand to one side, toward a corner of the room, so the audience subtends a smaller angle from your position. Take the time to show it from different angles if necessary, so no one is cheated.
Don't ask the audience to trust a measurement you make but they can't see. Consider projection analog scales or projection digital meters for electrical experiments. Avoid electronic balances; use visible mechanical ones. Sometimes all that's necessary to make a point is a visual indication of which direction something moves.
Color helps in many ways, to distinguish one thing from another, and just to enhance visibility. Why use a white paper sheet when paper can be had in many colors? Ping-pong balls and golf balls come in many fluorescent colors now. White or black string can be replaced with colored kite string, mason's cord (hardware store item), or rug-maker's cord. Water can be made more visible with a bit of food coloring, but tell your audience that you've colored it so no one will think it is something other than water.
Black lecture tables are drab. Consider having a selection of unpatterned tablecloths in attractive colors. Equipment stands out a lot better against them. Stand back in the lecture room to judge the effect.
Any well-equipped lecture hall has portable steps so the experimenter may safely ascend to stand on the lecture table for greater visibility.
Your students may be in the dark much of the time, but you, the experimenter, should work in a well-lighted environment.
Use all sensory clues. If you want to remind the audience that something is rigid, tap it on the table so they can hear it. Yank the string to show it doesn't stretch.
Demonstration list
 |
This document is an alphabetical listing of lecture demonstrations suitable for physics courses, with brief descriptions. I intend to continually add to this file. More demos, corrections, clarification and suggestions are welcome at the address shown to the right. Herbert H. Gottlieb contributed a large bunch to get the project started. As more come in I will flag each contribution with the author's initials and add them to the list of names and e-mail addresses.
I've included credit tags where I've used the exact details or text of a description supplied to me by a person or source, or when some particular idea of apparatus or presentation seems original to the person credited. Uncredited comments are my own.
Many of these references are old. This helps remind us that these demonstrations go back several generations. I have found many books of this kind in used book stores, flea markets and library book sales. Older ones are often reprinted and appear for a short time in mainstream bookstores.
In the spirit of Julius Sumner Miller's presentations, and his Millergrams books, I have added questions stimulated by the demonstrations, and sometimes I don't give answers! Readers are welcome to treat these as physics puzzles, and send me their own answers. The tag [Answer] links to an answer at the end of the document (so you won't peek at answers too quickly); the tag [<] links back to the question.
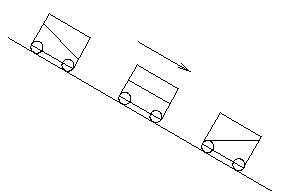ACCELEROMETER ON AN INCLINE.
Mount a liquid accelerometer on wheels. Predict the inclination of the water
surface as it accelerates down an inclined plane. Three possibilities are
shown. Explain what you observe, with free-body diagrams. [BERG]
Berg does this in his shows as a test of understanding. In a classroom situation I recommend that you first consider the acceleration on a level surface, to develop a clear understanding (with free body diagrams) of what makes the water surface tilt.
If you don't happen to have a liquid accelerometer, use a clear plastic glass or beaker mounted (fastened) on a suitable cart. Cover the top in case of a crash. Provide a method for slowing the device (or catching) it at the bottom of the incline.
Answer: The water level is parallel to the plane during constant acceleration. Imagine this as seen from the accelerating reference frame of the moving cart, in which the cart is at rest. This effectively removes from consideration the component of gravitational force that is parallel to the plane. (In this frame there's no acceleration parallel to the plane, so there's apparently no component of force parallel to the plane.) The only remaining force affecting the water is the sum of the component of gravitational force normal to the plane and the force of the bottom of the accelerometer . The water surface aligns perpendicular to this net force.
You can see this demonstration here.
In fact, in the picture above, the three situations, reading left to right are (a) the level as the acclerometer builds up speed from rest, (b) the situation at constant acceleration and (c) the situation as it is decelerating to a stop.
ADIABATIC HEATING. A considerable temperature increase occurs when a rubber band is stretched. Stretch a thick rubber band briskly and forcefully several times, then touch it to your upper lip.Your lip can sense the increase in temperature. Allow the rubber band to contract rapidly and note that it suddenly becomes colder. [HG]
AIR GLUE. To demonstrate Bernoulli's principle, cut a circular piece of cardboard slightly larger than the end of a thread spool. Push a straight pin all the way into the center of the cardboard. hold the spool so its hole is vertical. Press the cardboard against the bottom of the spool with the free end of the pin inside the bottom of the spool hole. Blow into the top of the spool hole. The air acts like glue and the card board clings tightly to the spool as long as there is air motion through the spool. [HG]
AIR PRESSURE SUCKER. Is so-called suction a push or a pull? Arrange a flask fitted with a two hole stopper and a glass tube extending well down into the flask that is completely filled with water. Challenge a good-natured student to "suck" water up the glass tube while the instructor holds a finger over the other hole of the stopper. When the student fails to get any water out of the flask, the instructor might remark, "Jim is not as big a sucker as we thought." After appropriate comments and removing the finger from the stopper hole, the instructor asks the boy to try again. Suddenly the sucker succeeds. When the class becomes orderly again, explain how air pressure provides the necessary push. [HG]
AIR PUCK. Cut a six inch circle of plywood or pressed board. Cement a small cork at its center, Drill a very fine hole through the disc and cork. Inflate a balloon and fasten its mouth over the cork. Place the apparatus on a smooth surface to see almost frictionless motion on cushion of air. [HG]
This is the budget method for doing collision studies on a near-friction-free surface. Disadvantages: The inflated balloon adds air drage. The balloon devlates in short order. Other methods use a very flexible hose to supply the air. Dry ice pucks are sometimes used. Of course commercial air tables are best, but take up a lot of storage space.
ALTERNATING CURRENT MADE VISIBLE. Method 1: Obtain a long, lightweight and flexible AC power cord with a plug on one end and bare wires at the other. Wire a small neon glow tube (of the sort used in night lights) with a 10K resistor in series and solder to the bare wires. Insulate the bare wires fully. Plug it in. The neon bulb should glow. Now swing the bulb round and round in a circle in a darkened room, and you will see that the glow isn't continuous. The two electrodes cause the neon gas to glow only near the peaks of voltage.
Method 2: As you watch a stationary neon bulb, sweep your gaze across it. Persistence of vision will leave a trail of bright dots. I've seen this trick also used with the spot from a laser beam reflected from a vibrating mirror onto a blackboard. The beam moves up and down rapidly, but the waveform can be seen against the blackboard by sweeping the eyes horizontally. A poor person's oscilloscope!
ANTI-GRAVITY. Select two test tubes so that one barely fits inside the other. Partly fill the larger with water and float the smaller one on the water. Quickly invert the tubes. As water leaks out, the smaller tube rises, apparently defying gravity. [HG]
But what about the relation of speed to mass? This may be studied quantitatively.
The cups may be nested, presenting nearly the same aerodynamical profile
for one, two or more cups. Drop one cup and a stack of two simultaneously,
from different heights. How much higher must you drop the stack so that it
lands simultaneously with the single cup? How about a stack of three? Someone
may have to stand on a ladder to drop the heavier stack. (Alternatively,
both may be dropped simultaneously from the same level, one landing on the
desk top, the other landing on the floor. Adjust starting level till they
land simultaneously.) In our experiments a stack of four must be dropped
from twice the height as a single one to land simultaneously. What does this
tell you about the relation between speed and mass? In these times of shrinking
equipment budgets a quantitative experiment such as this, which uses only
inexpensive materials, is most welcome. [Answer]
AUDIBLE ACCELERATION.
We cannot perceive acceleration of a falling body by eye. A classic way to
convince students that falling bodies accelerate uses wooden balls, metal washers,
or large metal nuts affixed to a
long cord that is hung from the ceiling. The balls are spaced apart so that, from
bottom to top, they get farther apart, just the right amount so that when the upper end is released the sound of their impacts hitting the floor is a series of clicks equally spaced in time. Start with balls at zero, 30 cm, 130 cm, and 2.74 m from the floor.
The bottom ball should always be initially touching the floor when the system is released.
This demo isn't often done because of the nuisance of the setup and hanging and releasing the cord from the ceiling. A more practical version uses Galileo's "diluted gravity" method, rolling a ball down a grooved track with a slight inclination. Obtain a 6 foot long extruded aluminum V-strip from the hardware store. Make a suitable block to incline one end a couple of inches above the lecture table. A metal ball will roll down the trough slowly. Students probably won't "see" the acceleration. But if you place small paper clips along one edge of the ramp, the metal ball will make a click as it encounters each clip. Now space the clips for equal clicks. It will now be apparent that the clips increase their separation down the track. Always start by releasing the metal ball from the same position and mark that position for reference. When you have perfected this, you may want to calculate the clip positions, and replace each clip with a small groove filed in the aluminum. These will be permanent, and will produce audible clicks. Galileo would have loved it. The apparatus is easily stored in the stockroom. [DES]
BALL IN FUNNEL. Blow into the small end of a funnel containing a ping
pong ball. The ball will not fall out even though the funnel is inverted,
so long as air is moving between the ball and the funnel wall. [HG]
Stores that sold vacuum cleaners used to attract customer's attension by setting up this demo with a vacuum cleaner blowing air through a funnel, and a lightweight colorful ball bouncing above the funnel, suspended there. Would this also work if the vacuum cleaner were reversed, to "suck" air through the funnel? Are you sure that isn't the way they were doing it?
This demonstration doesn't work reliably with balloons. The outcome depends
upon the degree of inflation of the two balloons. One could consistently
use the same brand of balloons, and practice in advance to get the correct
initial inflation, but isn't that something of a fraud? The demo is much
more reliable with soap bubbles, but more trouble to do.
The only excuse for doing this demonstration is to illustrate a detailed
calculation of the dependence of surface tension upon pressure. This is a
bit too much math (vector free-body diagrams in three dimensions) for most
high school courses.
Question: Why do balloons rise in the atmosphere? Answer: Because
someone let go of the string.
Question: Does an inflated balloon weigh more, less, or the same as
it does when deflated? By "weigh" we mean what it would weigh when placed
upon a sensitive balance scale. Answer: More. The air inside is
compressed. This may be easily tested with an electronic balance.
Showmanship tip: Inflate the balloon, tie it off, then fasten the
neck of it to the pan of the balance. Note the balance reading. Puncture
the balloon and note the change in the balance reading. Better yet, use a
sensitive simple mechanical balance, so that the audience can see
the scale unbalance when the balloon is punctured.
Serious question: When is a balloon hardest to inflate? Answer:
When it is smallest. Actually the pressure barely reaches 1.06 atm in the
early stages of inflation, then drops to about 1.05 atm and changes very
little from then to full inflation. That's why the two-balloon demo is so
unpredictable. Sometimes the two different size balloons just sit there,
without either one deflating.
BALLOON ELECTROSCOPE. Light rubber balloons suspended from long silk strings
act as demonstration electroscope. Charge the balloons by rubbing them with
woolen cloth or fur. When charged, the balloons can be made to stick to flat
surfaces such as walls or ceilings. [HG] With young children, consider adhering
the charged balloons to the clothing of a volunteer from the audience.
BERNOULLI ATTRACTION. [MG-1] Lay two books on the table with their spines
near each other and parallel, forming a channel on which two ping pong balls
can roll. Place the balls a short distance apart and blow horizontally in
the space between them. They roll toward each other.
BERNOULLI BALANCING ACT. Bernoulli's principle can be shown by balancing
an inflated balloon or beach ball on a jet of air from the output end of
a vacuum cleaner. The balloon will hover near the ceiling and will not fall
off even when the air jet is tipped at a considerable angle. A ping pong
ball balanced on a fine jet of water illustrates the same principle. [HG]
You can even lie on your back on the floor and blow upward to support a ping-pong
ball. Or blow through a vertical tube. Or stand up and blow through a tube
bent in a right angle, with the open end up. [DES]
BIG TORQUE. Hold the end of a broom handle in one hand and extend your arm
and the broom handle horizontally in front of you. Tie a string around a
book and hang the book under the stick a few centimeters from your hand.
Try to keep the stick horizontal while someone slides the book toward the
end of the stick. Although the weight of the stick and book do not change,
the torque increases. Lever arm has real meaning here.[HG]
Result: It stays at the same level relative to the surface. Even when
you whack the beaker from the bottom the float stays at the same level. Of
course a detailed analysis with a free body diagram is in order here, or
nothing will be learned from the demonstration.
BLACK BOX CONTENTS. Into a small box, place small objects and seal the box
closed. Students can manipulate the box, and try to tell you: (a) How
many pieces are in the box. (b) the shape of the pieces. (c) How heavy the
pieces are (density). (d) How big the pieces are. (e) The color of the pieces. By
doing this the student has reason to believe that scientists may know something
about the atom even though it has never been seen; just as the student knows
something about unseen objects in the box. [HG]
I recommend boxes with the following: (a) one wooden sphere, (b) one wooden or plastic cube (from a pair of dice), (c) one wooden rod or cylininder, (d) a small amount of sand, (e) some water in a closed bottle, (d) some with two or more objects, (e) a wooden ball attached with a cord to the center of one cube face, (f) a wooden ball attached with a cord to the inside corner. In the last two, the cord should be shorter than the cube edge, so that it can only touch the nearest faces of the cube. A chemistry colleague also used to make some cubes with inner compartments, splitting the cube into two equal chambers with a wall down the middle. [DES]
BOILING WITH ICE. Fill a flask two-thirds full of water and bring it to a
boil. Cork the flask and invert it, taking care that the hot water does not
spill out. Place an ice cube on bottom of flask. As the ice melts, the water
begins to boil again. If the flask is corked with a one-hole stopper with
a glass tube extended almost to the bottom of the flask, boiling can be effected
by reducing the pressure of the entrapped air. You can also run cold water
over the flask. Have the student feel the flask temperature as the ice boils
the water. [HG]
BUTTERED TOAST
If a slice of buttered toast is accidentally brushed off a tabletop, does it usually land buttered side down? Yes, but why? Buttered toast is messy, but this experiment works just as well with a wooden slab the size of a slice of bread, painted yellow on one side (simulating butter). Or any flat object with one side marked.
See also coindrop and dropping things.
[Answer]
BUTTON-AND-STRING SPINNER. Children used to make these as toys, using a large
coat-button from their mother's sewing basket. Loop a string or heavy thread
through two opposing holes of the button, and tie the ends together. Put
the loop over your thumbs with the button hanging. Spin the button around
until the strings are well-twisted on both sides. Then pull the strings taut.
The button will spin rapidly as the string unwinds. When nearly unwound,
release the tension, but keep the string relatively straight between the thumbs.
The angular momentum of the button will cause the strings to twist again
in the opposite direction. As the button slows, pull on the string again
and its spin direction will reverse.
This is more interesting to do than to watch. One learns to modulate the
tension during the spin for maximum performance. The tactile "feel" of this
process is fun to experience. If the button has slits or a raised repetitive
design it may make a musical "whirr" as it spins, the pitch being speed
dependent. Lots of physics here! You could even punch or drill equally spaced
holes just inside the rim, to produce clear tones.
This demonstrates conversion of energy from kinetic (spinning rapidly)
to potential (string "wound up"). There's considerable friction loss, so
one must continually supply energy by pulling on the string at the most advantageous
times. Compare this to the person pushing a child in a swing. The push must be
timed to be just after the maximum amplitude is reached. If you push just
before that you'll take energy away from the swinging system.
The string should be quite pliable, and not too heavy. In fact the optimum
weight/length of the string is dependent on the weight of the spinner. The
holes in the button should not be too close together.
Other spinners to consider: The plastic or metal gears or pierced disks from
Erector (TM) or Meccano (TM) sets work well. Colorful spinners may be constructed
from K-Nex (TM)construction sets. [DES]
Color mixing: Consider pasting colored sectors to one side of a
larger size spinner, using the three primary colors. When spun, you may get
white. The angular size of each sector can be adjusted until the white is
quite pure (the three color sectors won't be equal in angle). Mixing just
two sectors can give you green from yellow and blue, orange from red and
yellow and purple or magenta from blue and red. This is additive color mixing.
(Purple and magenta are not spectral colors, but are achieved only by mixing.)
[DES]
Persistence of vision: A different version of button-string-spinner
can be used. This uses a disk with four holes, in pairs of two on opposite
sides.Two strings connect to these holes, so that the card may be spun, not
in its own plane, but around its diameter. Experiment with hole spacing,
card weight, and string weight for best performance. Now two pictures are
put on opposite sides of the disk, which will be "mixed" when the disk is
spun. A common illusion is a picture of a bird cage on one side and a bird
on the other. When spun, the bird appears to be in the cage. Mixing of two
colors may also be demonstrated. [DES]
CHAIN REACTION. Arrange wooden matches closely on a soft board by means of
straight pins placed through them at their midpoint. Hold the board upright
and ignite the bottom match. The others will follow in turn to simulate
a chain reaction. The usual warnings about "playing with
fire" apply here. [HG]
Push pins through a thin board in a regular triangular array about 1 cm apart.
The board is in a vertical plane. Stick the back end of matches onto the
pins. Light a match near the bottom of the board. Chances are it will ignite
the two nearest matches above, and so on, demonstrating the multiplication
factor of a chain reaction. I have not tried this, but it could conceivably
work with the board in a horizontal plane if the matches are closely enough
spaced. This would be more realistic, in that the reaction would spread in
all directions from the initial match. But to make it visible by an audience,
a large mirror would have to be placed above, at a 45° angle.
If this is feasible, one might consider dispensing with the pins and using
a board of metal or other fireproof material with an array of holes drilled
in it to anchor wooden matches. The pins in the above demos were only to
protect the wooden board from being scorched. [DES]
Of course the best chain reaction simulation is still the large array of mousetraps,
cocked, with two corks resting on each one. The entire array is in a chicken-wire
enclosing box. Triggering one trap releases two corks (analogous to neutrons)
that bounce within the box and may trigger two other traps, which release
two more corks, and so on. When done properly, it seems that the whole thing "goes
off" in an instant, ending up in a jumble of mousetraps and corks.
CHIMNEY TOPPLING.
Old brick factory chimneys are demolished by explosive charges at their base.
If tall enough the chimneys do not topple as a single unit, but break in
two parts as they fall, at a point about halfway up. This may be easily
demonstrated with two wooden cylinders on a tiltable board, as shown. Children
demonstrate it with stacks of wooden blocks, doing physics at a very early
age. But they don't try to explain why it happens. Can you? [DES]
Show that this doesn't happen with a stack of two cubes. What does happen?
Now try higher stacks of cubes or cylinders. How high must the stack be before
you see the definite "breaking point" occur partway up the stack? What
conclusions can you draw? Does the area of the base relative to height play
a role? Does the cross-section of the stack at the point of the break play
a role?
COLOR ABSORPTION. Using colored pencils, draw a bird in a blue cage. Let
the bird out of the cage by covering the drawing with a red filter. Try other
color combinations to show the effects of color absorption by filters. [HG]
COLORED COCKROACHES. Many organic substances, dead or alive, show interesting
characteristics under ultraviolet (UV) light. Cockroaches are multicolored under
ultra-violet light. [HG] The "whitening" agents in laundry products cause
white shirts to glow in UV. Some postage stamps have hidden printing visible only in UV. Of course many rock and mineral specimens glow in various colors in UV.
CONDENSATION OF WATER VAPOR. A simple cloud chamber can be made from a gallon
jug fitted with a one-hole stopper with a short piece of glass tubing. Blow
into the jug through the glass tubing to increase the pressure. Put a finger
over end of tube and pull out the stopper, suddenly reducing the pressure.
No cloud is formed. If some smoke is introduced into the jug it provides
nuclei about which water vapor condenses. Repeat the performance and watch
the clouds form in the jug. [HG]
Presentation: "This is great for someone who never knows whether he's
coming or going." Walk with the red ball in front of you. "If the red ball
is in front of your face you are going." Turn around and walk the other way.
"And if the blue ball is in front of you, you are coming." [Dick and Rae]
COTTRELL PRECIPITATOR. Attach one lead from a spark coil to a foil surrounding
a glass tube of about one-inch diameter. Extend a wire from the other terminal
of the spark coil through the tube, insulated from the foil. Place a small
amount of hydrochloric acid in one flask and some ammonium hydroxide in a
second flask. With glass tubing connect the flasks and large glass tubing
in train. Blow air into the first flask causing ammonium chloride to be forced
into the Cottrell precipitator. Activate the spark coil and see 'smoke' consumed.
It works near instantly on cigarette smoke. [HG]
CRUSHED CAN. The force of normal external air pressure is sufficient to collapse
a rectangular varnish can. In a clean can place a few tablespoons of water
and bring it to a boil to expel the air with the water vapor. Close the cap
tightly as soon as water boils vigorously. Cool the can by dashing cold water
on it. Two comments: You don't need to run cold water over the can. Be sure
to stopper the can very soon after you remove the source of heat. If you
don't, the reverse effect happens. [HG] I've seen this done with 50 gallon steel drums. This quickly turns a useful container into scrap metal.
DENSITY OF ICE. Some properties of water make interesting conversation pieces.
Demonstrate that ice is lighter than water by placing a large icicle in a milk
bottle (ice cubes may be used). Add cold water to fill jar while holding the
ice under the water. Let the ice float and observe how much water overflows as
the ice melts. [HG]
DIMPLES AND PIMPLES.
[Use safety glasses and protect nearby
students with a shatterproof glass or plastic shield between them and the
experiment.] Heat a spot on a cold light bulb with a blow torch and
a dimple will form in the glass. Light the bulb and again heat a spot until
a pimple forms. [HG] The fact that the dimple is indented shows that there's lower pressure inside the bulb. If a bulb is broken, it doesn't explode, it implodes.
DISAPPEARING GLASS. Some liquids have an index of refraction very close to
that of glass. When a glass object is lowered into the liquid, it almost
disappears. For some materials the dispersion of the liquid doesn't match that
of the glass, so a faint rainbow image of the object still can be seen.
For safety and good effect, the best combination I've found is Pyrex (TM)
glass in Wesson canola oil. The oil is nearly clear; just slightly yellowish.
Small Pyrex beakers immersed in it show only a faint outline, but, of course,
the frosted label remains visible, like the grin of the Chesshire Cat. A
diligent search of the lab stockroom may turn up some pyrex glassware without
labels.
Clean the glass thoroughly to remove any surface film.
For the adventurous who'd like to use other materials, here's some information
from various sources. Some readily available liquids already are near-matches
for the refractive index of crown glass, which is 1.5170 for the sodium D
line.
Transparent solids
Transparent liquids
Also consider these combinations:
Some mixtures may be concocted by trial and error. Be careful,
because some of the ingredients are carcinogenic. If you use those, keep
them in sealed bottles and avoid skin contact or breathing the vapors.
The index of the mixture is not simply the average of the indices
of the components.
Variations:
Lower a glass stirring rod into the liquid. The portion below the surface
disappears. Lower the glass end of an eye-dropper (crown glass) into a liquid
of the same refractive index. The glass disappears, but the image of the
air inside punches into the liquid. Draw up some liquid. Remove the dropper.
Squeeze out drops, and it seems if they are drops of glass from the end of
the dropper.
Keep a small beaker in a stoppered bottle of the liquid. The beaker vanishes, but
its frosted label won't. Tilt the bottle so the beaker is partly exposed
to reveal that it's really there.
Let a coin rest on a small submerged transparent solid object. The coin seems
to be suspended in the liquid.
DROPPING THINGS. Here's a simple scenario to convince students of the importance
of words and of specifying things completely and precisely. Hold up a book
and a sheet of paper. Drop them simultaneously from the same height. Note
the behavior of the paper. Try dropping them with the paper dropped edge
down. The book wins each time.
Hold the book in one hand, paper in the other, hands wide apart. "I claim
that I am clever and skillful enough that I can drop both of these from the
same height simultaneously, yet the paper will reach the floor first." Students
are probably doubtful of this claim. Place the paper underneath the book
and drop it. "Not fair!" say the students.
"OK, this time I promise not to put the paper under the book. Yet I claim
that when the book hits the floor, the paper will be within 1 cm from reaching
the table." This time you put the paper in the book, between the back cover
and the pages.
"I can do better. I will place the paper on TOP of the book, then drop them together and the paper will reach the table first." Hold one finger under one end of the book, and release the other end so that the book rotates as it falls. Do this from a height of about 32 inches above the table. Experiment to get the ideal height so the book makes exactly 1/2 revolution. (See buttered toast.)
Finally: "This time I promise to drop them simultaneously from the same height,
one in each hand, so the paper never touches the book." After they agree
that this sounds fair, crumple the paper and wad it into a tight ball before
dropping. They land simultaneously.
DRY WATER. Let the student propose explanations why one can pick a coin from
the bottom of a beaker of water that has been dusted with Lycopodium powder
and not wet a finger. The beaker was filled with water and the powder dusted
over the water surface. [HG] Lycopodium powder is the pollen of the Lycopodium
fern. Frankly I don't have an explanation off the top of my head, and haven't
encountered one in the literature. [DES]
EGG PHYSICS Here's some eggcellent demos with eggs, which we used to do when
we were children, and so did our parents and grandparents. Some of these
appeared in the Chicago Sunday Times, March 24, 1940, collected and presented
by Martin Gardner.
Eggs, fresh or old, sink in cold water, at least in my experience. But they
are so near the density of water that dissolving sufficient salt (several
teaspoonsful to a glass) in the water will make them float. In fact, you
can get a tall glass cylinder, put some salt water in it and float the egg
on the salt water, then carefully add plain water so it doesn't mix with
the salt water, and the egg seems to float halfway between the surface and
the bottom. I'm not talking about cooking the egg here—that's another
issue.
As-yet untested proposal.
Since an egg is so close to the density
of water, how about using it in an oversize cartesian diver, visible from
the back row! You might have to salt the water a bit to make it barely float.
Cap the container, and squeeze its sides.
An egg in boiling water often rises to the surface because of convection
currents in the water. But why does it stay at the top? For the same reason
that large pebbles in a container of small ones rise to the top and stay
there when the container is shaken. The pebbles develop convection currents
too.
Balance an egg on end. You can do this at the dinner table on a tablecloth,
or on a smooth table surface. Surreptitiously make a small pile of salt.
Balance the egg on it, then blow the loose grains away. Only the grains wedged
under the egg (which are the only ones supporting it) will remain, and not
be noticed.
Second method. Shake the egg forcefully to break the yolk. Then the egg can
be balanced on its broad end because the heavier globs of yolk sink to the
bottom, lowering the center of gravity. This can prompt a discussion of the
center of gravity relative to the center of curvature and the conditions
for equilibrium.
To balance a hard-boiled egg on end, gently crush the shell at the end and
sit it there.
To tell a boiled egg from a fresh one, spin it on its side. The hardboiled
eggs spin longer. The fresh ones lose energy from viscous drag. But a fresh
one will spin longer when spun on one end around its long axis than it will
when spun on its side. Why?
Spin a fresh egg on the table. Stop its rotation momentarily with your finger,
then quickly release it. It resumes spinning for a bit. When you stop the
shell abruptly, the yolk and white continue to rotate. If you release the
shell before that rotation stops, viscous drag pulls the shell along with
the yolk and white.
Most people cannot break an egg by clasping it between their palms, with
the two ends touching the palms. Try this with one of the football
players or wrestlers in your class. If they fail, they will challenge you
to do it. And you can. How?
Coat an egg with soot from a burning candle. Immersed in a glass of water
it looks silver.
A hardboiled, peeled, egg can be forced into a milk bottle by the usual physics
trickery. Burn a wad of paper in the bottle. When the flame is established
strongly, quickly place the egg in the bottle's mouth. It helps to moisten
the egg first. As the air inside is heated it expands, forcing air out around
the egg. Then as the air cools inside, the pressure drops inside the bottle,
and the egg is pushed inside by the greater air pressure outside. The egg
can be removed by turning the bottle upside down so the egg blocks the neck.
Then close your lips around the bottle's mouth and blow into it, creating
enough pressure to force the egg out. It pops out surprisingly quickly, so
be ready to catch it. Note: Avoid any explanation you may have seen
in books that talks about the flame "using up oxygen" in the bottle, for such
processes have negligible effect on the pressure in the bottle.
Another as-yet untested proposal. How about an unpeeled egg in a bottle?
Soak an uncooked egg in strong vinegar until its shell softens. Then the
egg may be sucked into the bottle by the method previously described. Now
flood the egg with cold water till the shell hardens. Pour out the water
and let everything dry. The egg in the bottle now seems impossible. I have
not tried hardboiling the egg first, or boiling it after it is in the bottle.
Wrap a string around the egg. Try to burn the string with match or candle
flame. The string won't burn because the thermal energy of the flame is absorbed
by the shell and the string can't reach kindling temperature.
An egg can be tossed into the air and caught on a plate without breaking.
It takes practice. Martin Gardner says that performer Bill Talent used this
in his juggling act. He'd put an egg on the floor between his heels, jump
with both feet, propelling egg into the air behind his back, then catch it
on a plate held in one hand.
Of course, eggs are used in the so-called inertia demos. Fill four glasses
with water. Put them under the four corners of a flat tray with raised edges.
Roll up four playing-cards and secure them with rubber bands. Use them as
supports for four eggs positioned directly over each glass. Knock out the
tray with a sharp blow of the palm. Eggs will fall into the glasses. Water
can be put in the glasses if you don't want the eggs scrambled, but the water
will splash out on the table. The smashed eggs won't. (You hope!)
Write a message on the eggshell with a solution of one ounce alum to one
pint vinegar. The writing is invisible, but penetrates the shell. Boil the
egg. The writing still isn't visible, but when the egg is peeled, the message
is seen on the solid egg white.
No matter how hard you throw a raw egg into a curtain or suspended bed sheet
the egg will not crack open. Because the sheet "gives" as the egg makes contact,
the deceleration time for the egg to change its velocity to zero is fairly
long. Therefore the sheet applies a large stopping impulse (force x time)
with a very small force and a long time. However, if the uncracked raw egg
falls out of the sheet and hits the floor, it comes to a quick stop with
a large force and... An omelet or scrambled eggs anyone? [HG]
This one is more of a trick than a demo. One must be careful about doing
tricks in a class setting. This one can be used in this manner: "Here's a
demo that seems to defy physics. But of course nothing violates correct
physics. Sure it's a trick, but just like magician's tricks, there's a physical
explanation. So what is a physical mechanism that would make this happen?
What's your model of how it's done?"
First the preparation. Blow an egg. You all know how to do that, don't you?
If not, here's the method. Shake it to scramble the contents. Put a needle
hole in each end and blow into one of these to force all the contents out
the other end so you have an empty shell. Leave it a few days to let it dry
inside. Now that you know how to do it, blow another egg, for use later.
Actually, for these demos, I think it better not to make the holes
in the ends of the egg, but elsewhere.
Close one hole in the egg with wax or white glue. Enlarge the other hole
if necessary to allow fine sand to be put inside the shell. Close the hole
with wax or white glue. This "egg" will now balance on either end or in any
other cockeyed position. Use your ingenuity and balance it precariously on
things. This is the "obedient" egg, for it balances any way you want it to.
The other egg you have prepared similarly. It is to be the disobedient egg,
that will balance only one way. Decide, before you blow it, how you want
it to balance. Perhaps on the small end? Then be sure to make the needle
holes well-removed from the point of intended balance. This time mix finely
shaved candle wax with the sand and put some inside the egg. Close both holes
with glue. Let dry. Heat the egg, point down, till the wax melts and the
wax-sand glob is adhering to the inside of the egg-shell. Let it cool, and
it balances on its tip. Even worse, if you try to topple it, it comes right
back to its original balance position, just like those little clown toys.
A very contrary, disobedient egg.
Properly presented, it can eggsasperate students who try to figure out what's
going on. Practice till you are eggspert, and you'll get eggcellent response
from students.
If you don't want to bother with real eggs, consider using the colored plastic
eggs seen in stores around Easter-time, or the old L'Eggs (TM) containers
for panty-hose, or the small eggs silly-putty (TM) is sold in. Weights can
be glued at appropriate places inside.
Don't omit a mathematical discussion of how the center of mass must relate
to the radius of curvature at the table-top to ensure that the egg won't
roll to a different position. This is a good demo for illustrating conditions
of stability.
ELECTROSTATIC INFLUENCE I. Charge a glass rod by rubbing it with silk and
bring it near the thin stream of water from a faucet. The stream will
be deflected toward the charged object. Charge a rubber or plastic
rod by rubbing it with wool or fur, and the water will also be drawn
toward the charged object.
Presentation:
As always, be sure to sweat the details to get the maximum instruction from
these simple demonstrations. [DES]
ELECTROSTATIC INFLUENCE II. A charged comb attracts small scraps of paper,
or a piece of string or hair. Can it also affect a paper match delicately
balanced on a coin inside a glass? How does the electric influence pass through
the insulating glass? Touch the charged comb to the glass to find out. [DES]
EFFECT OF GAS DENSITY ON SOUND. Fill several balloons with different gases
such as air, carbon dioxide, natural gas, helium, and propane to about the
same pressure.Fix a whistle to be blown to a short piece of glass tubing.Note
the pitch as gas from the different balloons blows the whistle. [HG]
ELEMENTARY BATTERY. Show the emf produced between solutions of different
concentrations by using two copper discs attached to insulated wire and suspended
in a dilute copper sulfate solution, then drop a few crystals of copper sulfate
in to make the bottom layer more concentrated. Connect the electrodes to
a sensitive milliammeter or galvanometer. [HG]
ENERGY CONSERVATION. Suspend a bowling ball with a strong cord from the ceiling,
Draw the ball back against your nose, with your head against the wall. Release
it and stand nonchalantly awaiting its return. It cannot rise to greater
height from which it started. You are safe if you do not move or push
the ball during its release. [HG] Experienced (and daring) demonstrators
do this with the back of their head touching the classroom wall.
FALLING LEAKY BUCKET. A large Styrofoam (TM) cup is filled with water.
Punch a small hole in the side near the bottom and a stream of water shoots
out sidewise. Plug the hole with your finger before much has come out. Why
does the water shoot out this way? Because the weight of the water above
the hole causes the pressure just inside the hole to be above atmospheric
pressure, and the water near the hole moves from high pressure to low pressure.
What would happen if the cup were dropped from a considerable height? In
the cup's frame of reference it and everything else are accelerating at the
same rate and are (in this frame) weightless, so the pressure everywhere
in the cup drops to atmospheric pressure. Then there's no pressure difference
between the inside and outside of the hole, and no water shoots out. It's
best to this outdoors, from and upper floor window, and particularly entertaining
when a Dean or department chairman is walking beneath. If done indoors, from
a balcony or high ladder, have it fall into a plastic wastebasket. [DES]
Richard DeLombard suggests a very nice extension of this demo. First, he prefers a water bottle with a hole punched in it, being easier to handle than a styrofoam cup. Do not cap the bottle. Now ask students what would happen if the bottle were carefully tossed upward without spin or tumbling? After it leaves your hand, will the water come out the hole? If not, what will happen, and why? This is best done outdoors. [Answer]
FINGER FRINGES. Observe a line-filament lamp through the space between two
fingers, the fingers being parallel to the filament. Vary the width of the
space until you see a pattern of fine lines between the fingers. Such
line-filament lamps are about six inches long, have a single, essentially
straight filament and are unfrosted. They are sold for use in store display
cases. This demo can also be made to work by looking at a long fluorescent
lamp from across the room. A backlighted hand may look as if you are seeing
an X-ray of the bones of the hand. Observe objects through a bird's feather.
Here's the puzzle. What are these fringes? Diffraction patterns? Very likely they aren't. If
they were diffraction patterns they would show spectral colors. Too many "gee whiz" science demo books for children tell you that they are diffraction patterns. They lie. [Answer]
FISSION BUBBLE. Activation of a nucleus to cause it to fission may be simulated
by catching a soap bubble between two wire rings with handles. When caught,
puncture the top and bottom areas leaving a cylinder between the rings. Carefully
pull the rings apart, noticing the shape of the film, until it breaks in
two films over each circle. [HG]
FLAME DISCHARGE. Ionization in a flame can be shown by holding a lighted
match near a charged electroscope. Charged pith balls or balloons lose their
charge rapidly when a flame is brought near. [HG]
The answer is "none of these". The upper movable pulley drops till it hits
the bottom one. The forces don't add up. This illustrates the fact that you
can draw something on a blackboard that can't work in nature. It also reinforces
the advice we give to students in lab: Do the analysis using known physical
principles and make a prediction before undertaking the experiment.
I've seen students struggle for a half hour to make this system work before
they ask for help.
In case you were wondering, the whole system can be inverted, with the free
end pulling up. It doesn't work any better.
Some of us sneaky types like to treat this as a deception. We have the apparatus
set up with the load resting on the table. Then we pull on the free end and
the load rises. Best to do this after you've convinced the students that
it can't possibly work. Of course, you have pinned or otherwise gimmicked
the upper pulley so it can't turn. If the string slips on that pulley, coat
it with rubber cement.
GAMES. [HG] Games can make both learning and instruction a pleasure. Build
a puzzle of jumbled letters for other students to solve.An example:
GROWING SILVER CRYSTALS. Place a copper penny on the glass slide of a
micro-projector. Put silver nitrate solution around the penny and watch silver
crystals form on screen. Note the many peculiar characteristics they exhibit.
[HG]
GYROSCOPE, LARGE. Weld bicycle axle nuts into one end of each of two iron
pipes. Screw the pipes onto the wheel axle for handles. This makes an excellent
gyroscope. It's even better when the rim is weighted by winding it with iron
wire. Or fill the tire with sand for greater weight. [Be
very careful not to get your fingers in the whirling spokes, for the weighted
wheel has considerable inertia]. [HG]
GYROSCOPE BAT CIRCLES. While standing or sitting on a rotating platform,
turn around by swinging a baseball bat in circles over your head. Reversal
of the swing reverses the motion of your body. [HG]
GYROSCOPE HOME RUN SWING. Show action and reaction by standing on the rotating
platform and swinging a baseball bat vigorously at a pitched ball. This should
be amusing. Do it outside, of course. [HG]
GYROSCOPE MOMENTS. Again on the rotating platform, pirouette. Hold heavy
weights at arm's length, have someone rotate you slowly. When you are "up
to speed" bring the weights close to body. Explain the marked increase in
speed. [HG] [The speed increase can be great enough to disorient
an inexperienced person, causing them to lose balance and fall off the
platform.]
GYROSCOPE PLATFORM. Construct a rotating platform from an automobile front-wheel
and spindle. Rigidness, coupled with small friction and small play in the
bearings is amazing. This is useful to demonstrate rotational inertia and
maneuvering in space. [HG] There's great value in having each student do
this to feel the direction of the reaction torques. If this isn't
practical, the demonstrator should describe in detail what direction the
wheel seems to "want to move" as one tries to make the wheel move in a particular
direction.
GYROSCOPE PRECESSION. Stand on a rotating platform holding a spinning gyroscope
wheel with its axis horizontal. Observe what happens when the axis is rotated
to a perpendicular position to the right? To the left? [HG]
HAIR RADIO TRANSMITTER. Combing dry hair near the aerial of an AM radio produces
static. [HG] You could call the static "long-hair" music, but that joke is
lost on younger people.
HEAT TREATMENT. The effect of heat treatment and tempering of metals can
be demonstrated by heating bobby pins to redness in a Bunsen flame. Dip one
heated pin in cold water to chill it. Allow the other pin to cool slowly.
Compare these pins with one that has not been heated, by bending each one.
[HG]
HEAVY FINGER. [DES] This is an old demonstration, but
I think it is still worth doing and deserves special attention to its
presentation. Use an old-fashioned double pan balance. Don't be tempted to
use an electronic balance, for the students must be able to see the
changes. A beaker of water is on one pan, balanced by weights on the other
pan. Propose this question to the audience: "Suppose I were to stick my finger
down into this water, being very careful not to touch the sides or bottom
of the beaker, what will happen?" If there's any hesitation, or confusion
say, "It's really an easy question! What will happen is that my finger will
get wet."
"But that's obviously not what I meant. Let me phrase the question more
carefully. Will the pan with the beaker move down, up, or would the scales
remain balanced when I insert a finger into the water?"
During the discussion, demonstrate that if you press a finger on that pan,
it goes down. If you press on the edge of the beaker, it goes down. "But
if I'm careful to touch only the water, not the beaker, what happens?" Refuse
to actually do it till serious discussion ensues.
Finally, do it. The pan and beaker move down. "Why?" you ask?" Don't peek
at my answers until you've come up with at least two instructive answers
of your own. [Answer]
An alternate version uses two incline ramps at the left to achieve equal
velocities of the balls. I made one 5.5 feet long of steel construction set
parts (Meccano, Erector, Steel-Tech, Temsi, etc.). It includes two parallel
45° 10 inch long inclines at the start of the track to give the balls
equal initial speed. The lower level portion of the track is two feet long,
and is 5 inches lower than the upper track. The smooth, curved rise is about
a foot long horizontally.
Which ball wins the race? The balls gain kinetic energy on the first incline,
the one with the longer incline gains an additional kinetic energy of mgh
compared to the other ball. h is the height difference between the horizontal
portions of track. So the lower ball is ahead of the upper ball on the horizontal
tracks, and having higher speed, continues to gain its distance lead over
the upper ball. On the final rise, the lower ball loses as much kinetic energy
(mgh) as it had gained early on, so on exit they have the same kinetic
energy and the same speed. But the distance advantage the lower ball gained
going at higher speed on the straight track ensures that it wins the race.
This is a version of the famous "Brachistochrone Problem" first solved by
Johann Bernoulli in 1696. It is discussed in most intermediate mechanics
books. The problem was to determine what curve of incline will get an object
from point A to point B in the least time, when A and B are at different
heights. The curve of least time is a cycloid. Such problems led to the
development of the calculus of variations. [Answer]
"HOLEY" WATER. Do molecules of water have spaces between them? Pour water
into a long test tube or graduate until it is three-fourths full. Then completely
fill it to capacity with alcohol. Place your palm over the top of the container
and invert it. Be careful that no liquid is lost as the water and alcohol
mix. Observe that the container is no longer full. Evidently some alcohol
has disappeared in water molecule holes. [HG]
HOT DOG WHISTLE. Tune two metal dog whistles to unison or absence of beats.
Heat one whistle with a flame. Beats reappear as the pitch of the heated
whistle rises. [Please don't burn your lips!] [HG]
HOT ROD BALANCE. Drill a brass rod for a screw in one end. Insert a screw
about half way. Balance the rod at its center on a pivot. Throw off the balance
by moving the small screw out. Heat the other end of the rod and it comes
into balance again. [HG]
HYDROSTATIC SCALE. Weigh yourself by hydrostatic pressure. Use a hot water
bottle with a stopper fitted with about two meters of rubber and glass tubing.
Fill the bottle with water and connect the tubing so that it extends vertically.
Lay the bottle on the floor and cover most of it with a small board of known
area. Stand on the board and measure the increased height of the water in
the tube. Your weight is equal to the area of the board times the water pressure
increase. Calculate the water pressure by multiplying the density of water
(1 gram per cubic centimeter) by the difference in the water level height
when you stand on the scale. [HG]
HYDROSTATIC PUZZLE. [MG] A cork or wood ball floats on water. Add a layer
of oil to the water surface. Does the floating ball rise, or sink, when the
oil is added? Answer: It rises. Why?
Answer: It jumps inside the cup. In free fall, in the cup's frame
of reference, the ball is weightless, and it was its weight (the force of
gravity upon it) that was countering the upward tension of the rubber band
when the cup was at rest (as shown in the diagram). As the cup falls, the
tension force, unopposed, pulls the ball up and over the rim into the can.
[BERG]
INTERRUPTED PENDULUM. Show conservation of energy in a swinging pendulum
by noting that the bob returns to the same level each time. Place a peg or
obstruction below the point of suspension so that the arc of swing will be
changed to a shorter radius. Locate the peg at a point one half the distance
between the lowest and highest levels of the bob and then do it again with
the peg still lower. Explain why the bob loops over the peg. [HG]
INVISIBLE THWACK. [MG] Bend a playing card and stand
it upright. Stretch a rubber band on another playing card perpendicular to
it. The two cards are about a centimeter apart. The far end of the band is
pulled back and released. The standing card is knocked over, even though
you can't see that anything touched it. The front end of the rubber band
actually moves forward, breaking contact with the card. But when does this
happen, and why?
Presentation: A more durable apparatus consists of two large nails
in a board, the rubber band being stretched over them, and a card of any
sort set upright a short distance (about 1 cm) beyond one of the nails. First
snap the band without the card in place. Ask students to describe the motion
of the band in detail. They usually will not suggest that the front of the
band never breaks contact with the nail. Raise the issue. Then do the card
demo to confirm your hypothesis. Some may still doubt that the band hit the
card, thinking perhaps that you jiggled the table or the board, or even blew
on the card to knock it over. If they don't suggest this, suggest it yourself.
"How can we test the hypothesis that the band knocked the card over, when
our eyes can't see it do that?" Substitute a sense that isn't as easily
fooled as the eye. Have a student put a finger where the card was, to feel
the band hit the finger.
One answer is commonly seen and seems superficially plausible: When the band
is stretched, the front nail (B) exerts a force on it, but your hand balances
that force. When you release the band, there's an unbalanced force of the
front nail (B) forward on the front end of the band. This gives a forward
impulse. The momentum of the band is forward, and its center of mass moves
forward faster than the band can relax to its unstretched position.
I must admit that I was taken in by this bogus answer. I had forgotten that
it takes some time for the front end of the band to "know" that the other
end has been released. That is, it takes some time for any physical effect
of the release to reach the front end.
But the real answer is more interesting. Loren Winters and Travis Williams
at the North Carolina School of Science and Mathematics have taken high speed
photos of the band in action. These may be seen at this
projects in high speed photography page, along
with other fascinating pictures of physical phenomena.
They did more investigation to answer these questions:
Does the forward motion from nail (B) begin only after the band is fully
relaxed or when the moving end hits the nail (A), or the compressional
wave from end (A) has reached (B)? What if nail (A) weren't there?
They found that the pulse that knocks the card over occurs after the end of the band that was
pulled back reaches nail (A), and a compression pulse still moves forward past nail (B) toward the card.
In fact, only one supporting nail (B) is necessary.
This illustrates the principle that you should never give up thinking about
a problem just because you've gotten what you think is a plausible answer.
Even if you have a correct answer, there are always other ways to
arrive at it, and some of these may give you more insight.
The explanation of the SLINKY DROP demo is related
to this. Both are examples of a general principle. Changes in one part of
a system cannot affect another part of the system until some physical influence
passes from one part to the other. Such influences do not travel instantaneously.
One common source of mistakes in doing mechanics problems is to assume (without
thinking about it) that when the force is removed from one end of the rubber
band or spring that the other end "knows" about it instantly.
IMPULSE AND INERTIA MAGIC. Done with graceful flourish, this brings down
the house! The mechanics of friction, forces and inertia involved stimulate
interesting discussion. Set a glass two-thirds full of water about three
inches from the edge of a table. On the glass place a pie tin. On the pie
tin and directly over the glass place a spool on end. Place an egg (fresh
if you are confident) on the spool. With one foot on the bristles of a springy
broom, pull back the handle and aim at the pie tin. The spool rolls on the
table, the pie tin scoots to the floor, the glass and the water remain unmoved
on the table with the egg unharmed in the water.Note: The pie tin overhangs
the edge of the table. The table edge stops the broom's forward motion before
it hits anything else. [HG]
The wood block must be at least as high as the edge of the pie tin.
Variations. Only your imagination limits the possible variations you
might try. With practice, you can snatch the pie tin quickly enough with
your hand, using a smooth arm motion. Don't hesitate.
Which string will break when you jerk the lower string? [BERG]
This is a variant of the demonstration using only one ball and two strings,
say the top ball and strings A and B in the diagram. When B is pulled slowly,
A breaks, because the tension in A is larger than that in B by an amount
equal to the weight of the ball. When B is jerked its tension rises almost
immediately to the breaking point, while the tension in A rises more slowly,
since it takes a short time for the heavy ball to move and stretch string
A enough to reach its breaking point. The reason for the time delay is that
in F=ma applied to that mass, m is large, so
a is small.
To really understand this demonstration one must remember that a string doesn't
break until it is stretched (elongated) to its breaking point.
In these "inertia" demos involving jerks (including the tablecloth yanking
demo) one must consider the rapidity of the motion, and the fact that the
duration of the force can be smaller than the time it takes to move something
enough to cause a particular outcome. [DES]
Also see: Ehrlich's comments [Ehrlich, Toast] p. 16, and Arons' comments
on so-called "inertia demonstrations". [Arons] sec. 3.22. Arons concludes
that "Without visualization of the stretching of the strings, students acquire
no understanding of the demonstration; they simply memorize, and repeat,
that it had something to do with 'inertia.'" [<]
JERKS. [DES, MG] Quite a number of
demonstrations depend upon impulses of brief duration. The classic demo of
this type is the one in which a tablecloth is yanked from under a full table
setting, plate, silverware, glasses of water, etc. without toppling or spilling
anything and without moving the table setting to a significant velocity.
Use a silk or smooth rayon cloth, and be sure that the trailing edge has
no hem. It helps to roll up the edge you are pulling all the way to the edge
of the table before yanking it, helping to ensure that the cloth doesn't
"bunch up" anywhere during the yank.
Of course each object does move a bit. They move during the brief time while
the tablecloth slides from under them. Then, this motion continues as they
are brought to a stop by friction against the tabletop. It is important that
both the cloth and the tabletop be smooth and low-friction. If the table
surface slows them too quickly, tall objects like glasses and candlesticks
can topple forward.
Silverware can cause problems in this demo, and is best avoided.
Often this demo is passed off with the explanation. "The objects are not
disturbed because of their inertia." This explains nothing. When the tablecloth
is pulled slowly, everything moves along with it. If it is pulled more rapidly,
the wine glass topples. If it is pulled (yanked) very quickly, nothing is
seriously disturbed. Why?
The force an object experiences is that due to friction between it and the cloth,
and that friction is proportional to the normal force (equal to the object's
weight) and the coefficient of friction. The coefficients of static and sliding
friction aren't different enough in size to account for the outcome of this
experiment.
The impulse given by the cloth to an object on it is Ft, where
F is the tension in the cloth and t is the duration of application
of the force. The impulse changes the momentum of the objects on the cloth.
F depends on the friction force, and this is nearly independent
of the speed of movement of the cloth. Since the friction is proportional
to the normal force, which is constant in all cases, the impulse depends
only on the time, and if the time is short enough the impulse is small. Therefore
it is the impulse that is the key to the understanding of these experiments.
One can also argue that the cloth is removed in a time shorter than that
required for the objects to accelerate much. This is really the same as the
explanation of the previous paragraph. But one must still emphasize the
importance of the fact that the normal force is independent of the horizontal
force and also independent of the time of application of the horizontal force.
As always, in elementary mechanics courses, draw the free body diagrams as
you talk.
See: Ehrlich's comments [Ehrlich, Toast] p. 16.
[<]
Other objects may be used: a lighted candle, a smooth-edged coin balanced
on its edge, a smooth wooden ball. Try the coin trick with the coin in a
plane perpendicular to the yank, and also parallel to the yank. For a brisker
yank, hold the paper out horizontally from the table and do a downward karate
chop on it with your finger (Fig. d).
A little more suspense. Balance that glass of water, on the paper, sitting on your
head. Be sure the bottom of the glass is dry.
Then yank the paper. Practice, using a plastic tumbler. You have to
hold your body still while doing the yank. Easier: do this on your palm,
with a dollar bill under the glass on the edge of a table. Yank out the bill. (Dinner-table
entertainment!)
I have three brass cylinders of different weights and sizes, the largest
being an inch in diameter. I set them on the paper. "Big inertia, medium
inertia and small inertia" I say. They are so "touchy" that the slightest
motion of the paper makes them roll. Then I do the karate chop move to yank
the paper from under them, and none of them even jiggle. So what does this
teach us about inertia? Nothing.
So, do any of these "demonstrate inertia"? All objects on the cloth or paper,
whatever their mass, seem to behave the same. Even a lightweight folded napkin
in the table setting behaves the same. So these aren't clear
demonstrations of the property of inertia. But they are nice
demonstrations of impulse.
As one student observed, when asked to explain this, "If you apply a force
quickly enough to something, it doesn't notice." At least that's a better
description of what happened than "It was because of inertia."
LENZ'S LAW. Lenz's Law may be demonstrated with any toy wheel of nonmagnetic
material and low friction attached to a convenient holder. The wheel should
have spokes for clearest understanding. Spin the wheel in air then between
the poles of a reasonably strong horseshoe magnet. Spokes cut lines of force,
the induced current field opposes motion. [HG]
A meter stick is good for this demo. One can even tape a weight at some point
on the stick and it still works. A two-dimensional version: Use a large dinner
plate, with objects on it, perhaps even a glass of water. Use three fingers
spread wide to support it. Bring the fingers together! Your fingertips should
be dry. [DES]
A mathematical analysis of this can be found in Arnold Sommerfeld's
Lectures on Theoretical Physics, Volume 1, Mechanics Academic Press,
1964, pp. 83-85. It's a good exercise in forces, torques, and friction.
MAGNETIC WAVES. Suspend a bar magnet on a string. Rotate another magnet under
it to show transfer of magnetic energy. What changes the direction of the
poles? How can the change be effected without human movement. [HG]
MASS SPECTROGRAPH. Properties of alpha, beta, and gamma rays may be simulated
by propping a smooth board of about eight inches by twelve inches on an incline
and arranging a bin with a trap gate at the top so that three different sized
balls can be released to roll down the board. Place a strong magnet below
the board and just to one side of the gate. Note how each falling ball goes
into a separate bin because of the amount of deflection. The gamma may be
represented by a brass or aluminum ball, he beta would be the smaller of
the steel balls. [HG]
MATCH DISCHARGE. Rubber bands or strips can be tied together in bundles and
charged by stroking with fur or by other means. A lighted match near the repelling
strips will cause them to collapse. [HG]
MATCH HEAD DIVER. A Cartesian diver can be made with a Coca-Cola bottle full
of water and a match head. Continue cutting or breaking off the match stick
until the head barely floats. Thumb pressure on the mouth of the bottle makes
these little divers zip up and down in the bottle. [HG] Experiment with glass
bottles with secure plastic caps. Large medicine bottles with flat sides
can be pressed on the sides to make this work, since glass is slightly flexible.
There's no surprise in doing this with plastic bottles. Presentation
note: Since so many plastic bottles are made to look like glass ones,
tap the bottle on the table to let the audience hear that it is glass.
MIRROR IMAGE REVERSED? Why does a plane mirror seem to reverse your image
left-right but not up-down? This frequently-asked question has value for
encouraging students to think more precisely and use words carefully. Why
should this question even be interesting? Where's the "problem"? The discussion
shouldn't be carried out entirely in the abstract. Have a large mirror to
demonstrate. Rotate the mirror around its normal as a student looks at the
image. The image doesn't rotate. The mirror seems to be operating with axial
symmetry. Then why should the mirror treat up/down differently than right/left?
(Some students will even suggest gravity has something to do with it, so
have such students look in the mirror and lean their heads sidewise.) Have
one student look into the mirror while another stands behind the mirror looking
at the first student. Have each touch the top of their heads. Have each touch
their right ear. Perhaps have each wear something distinctive on the right
ear.
NUT DROP. Tie six or seven metal nuts on a string at distances in proportion
to (1/2) gt2 where the time is 1, 2, 3, 4, etc. seconds.
Hold the string vertical and still and then let it drop. Note there is no
difference in the time intervals as nuts strike the floor. [HG] To get full
value from this demonstration, have another string with nuts tied on it with
equal spacings. Drop it first, to demonstrate that the sound of the impacts
with the floor do not occur at equal time intervals. Here's a conclusive
test of the Aristotelian vs. Galilean laws of motion; a test accessible directly
to the senses without the need for timing devices. In a large room it's worth
putting two pulleys near the ceiling to hold the strings of nuts until they
are released. Or use light threads over supports near the ceiling to suspend
the two strings of nuts, then cut the supporting threads. [DES]
Follow-up question: What happens if the rotation direction of both wheels
are reversed?
This homework problem from Kleppner and Kolenkow may be demonstrated. I made
a model from Erector set parts. The rollers are 1 inch pulleys with thick
rubber o-ring tires. The rollers are about 6 inches apart, driven by a pulley
arrangement with a long rubber o-ring belt, driven by a standard Erector
set motor geared down to slow speed. The beam is a 10 or 12 inch angle girder.
Place the girder on the rollers so that its angle is like an upside down
V: ^. When the rollers turn, the girder oscillates back and forth with simple
harmonic motion, without falling off the rollers. This is just as predicted
by the mathematical analysis. Sometimes the friction is a bit erratic, but
the girder stubbornly refuses to fall off. I've had a model in a display
case with a button to activate the motor, and many people have tried to topple
the girder without success. Of course, if the motor were reversed, both rollers
turn the other way, and the girder smoothly moves in one direction and falls
off.
Some students argue that sometimes, once in a blue moon, the stopping position
of the girder would be just at a balance position, and when the motor is
started again the girder would just sit there without moving in either direction
as both wheels slid underneath it. It has never happened yet. This must be
telling us something profound about how nature works.
This is related to the "locating the center of gravity" demo in which you
support a meter stick with two fingers, then move the fingers together.
PAPER KETTLE. Boil water in a paper cup. The paper will not burn until the
water has boiled away. [HG]
The usual explanation: The paper has been smoothed down over table
and slat. Some books simply say that
the pressure of the air downward on the slat is what secures it in place
on the table. If that were all there were to it, the paper would not be needed.
If the paper is carelessly placed and not smoothed down, this shouldn't work,
according to the usual explanation. Any correct explanation must include the
fact that smoothing the paper helps prevent air from getting under the paper easily.
The paper is somewhat flexible, so when the shingle is struck, the portion under the paper
rises a bit, creating a space with very low air pressure. The force on the slat is now
unbalanced, with much greater force of air pressure above. If the slat breaks before
air has a chance to flow into the space under the paper, the demonstration is a success.
Consider the old experiment in which two of the rubber flat sink-stoppers
(about six inches diameter) are pressed together, then one attempts to pull
them apart. (The poor man's Magdeberg hemisphere experiment. If you are even
poorer, use one stopper on a smooth tabletop.) If the stopper surfaces are not very smooth,
they pull apart easily. But if you sand them with very fine emery paper,
or moisten them, they are difficult to separate. Can we say it is simply
the air pressure that prevents them from separating? No. The fact that they are
flexible, allowing creation of a low pressure space between them, is essential.
The fact that air can't easily get between them is also essential. So what
did Magdeberg demonstrate in 1654? He used iron hemispheres, and deliberately
used the newly invented air pump to remove most of the air between them.
Could we separate the two hemispheres
(or sink-stoppers) if they were surrounded by a vacuum?
But this demo of breaking of the slat is misleading. Demonstrate it using a
wooden yardstick lying on the table with a bit of overhang. Strike the overhang
with your hand, and the stick goes flying up in the air. Now replace the
stick and strike the overhanging portion forcefully with a broomstick. The
end breaks off. No newspaper is needed! I often do this with old strips of
lath of the kind used in old houses under plaster walls. This may also be
playing a role in the usual demonstration.
Explanation of the paperless breaking demo: Air pressure plays no role
in this version. This works best if the portion of the lath lying on the
table is long compared to the overhang. The blow to the overhanging end gives
an impulse of short duration. This stresses the overhanging end, as it starts
to bend. The internal stresses cause a wave of stressed wood to move toward
the table. When this reaches the edge of the table the wood is forced down
against the table edge, and an upward reaction force from the table acts
on the wood. This force and the downward force of the broomstick act as a
couple, tending to rotate the portion of the yardstick extending beyond the
table. The more massive portion of the yardstick has not yet received any
of the stress wave, and has not yet been acted on by any forces tending to
cause it to move up away from the table. Crudely, "It doesn't yet know anything
has happened." The yardstick breaks before the longer portion has a chance
to move.
PENCIL POINT BALANCE. To demonstrate center of gravity outside of a body,
and the criterion for stability, borrow two pocket knives from students.
Push the blades firmly (but carefully) into a pencil near the sharpened end
with the handles beyond the point of the pencil. Balance the pencil point
on your finger. Since the system's center of gravity falls below the point
of balance, the system is stable. [HG] Today, students are not allowed to
carry knives in schools. How times have changed! When I was in school in the
1940s and 50s, nearly every boy carried a pocket knife, for whittling, playing
mumbledy peg, trimming wooden slingshots made from tree branches, and sharpening pencils.
And I never heard of a case where a knife was used as a weapon. [DES]
PINHOLE EFFECTS. An interesting conversation piece can be made from an empty
35 mm film can. In the center of one end punch one hole with a sharp needle.
About the center of the other end punch three pinholes at the corners of
an equilateral triangle about two millimeters apart.Look through the one
hole and see the three holes. Look through the other end at the one hole
and explain what is seen. Label the box "Drunk-O-Meter" and list the following
directions: 1 hole—sober, 2 holes—nipping, 3 holes—dog drunk,
4 holes or no holes at all—dead drunk. [HG]
POURING CARBON DIOXIDE. Construct a series of three 5-cm steps that will
fit into a wide mouth jar. Set a lighted candle on each step. Slowly pour
carbon dioxide gas from an open container into the jar. Carbon dioxide is
heavier than air. As it settles it extinguishes the candles one by one starting
with the candle at the lowest level. There are many ways to generate carbon
dioxide. Try mixing some vinegar with bicarbonate of soda. [HG]
PRECISION IN ADVERTISING. Encourage students to think, speak, and write more
precisely. Illustrate by using a meaningless advertising slogan: "The
Rolls-mobile is bigger and better than (a) a kiddie car (b) a freight car
(c) last year's model. [HG]
RATE OF HEAT CONDUCTION. Three students, each holding a rod of a different
substance in a flame, will demonstrate the difference in conductivity of
heat by their object from the flame. Use about the same sized rods of iron,
aluminum, glass, copper. [HG]
REACTION OF THE ROAD. Place a plank on rollers (doweling). With a string,
tie a small cart to one end of the plank and stretch a long rubber band between
the cart and the other end of the plank. Add weights to the cart to increase
its mass. Burn the string to release the system. The road goes one way, the
cart goes another. [HG]
RETINAL AFTER EFFECTS. Draw a circle in the center of a piece of white paper
with colored crayon. Stare at the circle at arms length for a time, then
look at a blank wall. A circle of the complimentary color appears on the
wall. [HG]
The case where the spool rolls toward you as you pull on the ribbon often
seems counter-intuitive to students. The spool is moving faster than the ribbon pulling it. But on reflection, isn't it equally counter-intuitive that in other cases the spool
rolls opposite the direction you are pulling? This demonstrates once again that
our naive intuition often misleads us. More advanced students might want to work out the energy conservation implications of these cases.
[DES]
A variation, to challenge the better students: Find a suitable sized cylindrical
solid object. Tape one end of a length of cash register tape to it and wrap
the tape around it's circumference. Now pull on the tape. The cylinder rolls away from you,
as expected. Now bring the tape to the table top, and if you are very, very,
careful, pulling slowly, the cylinder slides toward you without rolling. Doesn't
this seem to defy what we learned above about the angle of pull? What's going
on here? The tension of the tape exerts a horizontal force on the cylinder,
but that's matched by the friction force, so there's no net horizontal force,
and no acceleration. The only torque on the cylinder is the tension of the
tape, with a lever arm equal to the radius of the cylinder. That torque should
produce a constant angular acceleration. But we observe no angular acceleration,
and no angular velocity. Is some physics being violated here? (A large roll
of cash register tape is fine for this demo if you can still find one.) [DES]
[Answer]
Challenge trick: When you've gotten the feel of this, tell students
that you can actually make the solid cylinder roll toward your hand. Use a
long lecture table, and slowly accelerate the system, so the cylinder slides
without rolling. Then suddenly stop. The cylinder's inertia causes it to
roll toward your hand. [DES]
SEEING THE SUN BEFORE SUNRISE. The fact that one may see the sun while it
is still below the horizon can be simulated by looking at a penny at the
bottom of a bowl filled with water.Note that the penny cannot be seen over
the rim of the bowl unless there is water in the bowl. When the sun first
appears in the morning, it is still our of sight below the horizon. Refraction
of the sunlight by the atmosphere makes the sun appear higher than it really
is. [HG]
SELECTIVE LIGHT SCATTERING. Demonstrate the effect of the sun setting through
the dust-laden atmosphere. Add five grams of sodium thiosulfate and 5 mL
of concentrated hydrochloric acid to a liter of water in a clear container.
Shine a light through the solution and on to a wall or screen. Observe the
changes as the colloidal sulfur forms. Scattered blue light can be seen in
the solution at a ninety degree angle from the beam.On the screen or wall
the spot slowly changes from white to yellow, to red, and then is finally
is blacked out completely. [HG]
SHADOW REFRACTION. Place an object on the bottom of a metal pan so that its
shadow may be measured. Fill the pan with water and remeasure the shadow.
Refraction is evident if the pan, object, and light source are kept stationary.
[HG]
SINGING FLAME VARIATION. Hold a four foot 1-1/2 inch glass tube vertical.
Insert in the bottom end at a predetermined resonance point a heavy disc
of wire gauze. Heat the wire gauze with burner, then remove the flame and
hear a phenomenon. [HG]
SINGING TUBES. A straight metal blow pipe connected to a gas supply is fixed
in an upright position on the demonstration desk and lighted.A thirty to
sixty centimeter glass tube of large diameter is lowered over the flame until
at a certain position a sound is heard. [HG]
SKY HOOK. Cut a four inch piece of wire from a coat hanger.Bend one half
inch back on one end so that a leather belt will slip in the hook. Rest the
free end of the wire on a finger tip. The belt and wire will hang out in
space without apparent support underneath. [HG]
SLINKY DROP. [BERG] Stand on the lecture desk for extra
height. Hold a SLINKY (TM) spring at one end. The other end shouldn't reach
the floor. Ask what will happen if you release the upper end. Of course all
will agree that the center of mass of the unsupported spring falls with acceleration
g, and that the spring begins to contract when you let go of it. But what
are the relative motions? Among the possible outcomes:
The outcome surprises students. The lower end remains at rest at constant
height until the rest of the Slinky closes completely, then the whole thing
falls to the floor. The center of mass of the spring falls with acceleration
g. In the center of mass frame of reference; the spring collapses
toward its center of mass.
Note that the acceleration of the upper end of the spring is initially
approximately 2g. When the spring is hanging, the center of mass is
not at its midpoint, but is lower because each part of the spring must support
the weight of everything below, so the separation of the coils is greater
in the upper part than in the lower part. Does this affect the outcome? Why,
or why not?
But without getting mired in these details, we know that the lower end cannot
react until information reaches it from the top end. At the instant the upper
end is released, the lower end "doesn't yet 'know' anything has changed."
No physical influence from the upper end reaches it immediately.
For more instructional value, show the students the speed of a compression
pulse along the Slinky. With the Slinky stretched, compress a small portion
near one end and then let go. The pulse travels to the other end slowly enough
to watch. The same thing happens when one end is released. The weight begins
to fall only when the compressed portion travels from one end of the Slinky
to the other end. So long as the coils at the left end of the Slinky have
the same spacing they had initially, the tension there is the same as it
was initially, thereby holding the weight (W) in static equilibrium.
A follow-up question comes to mind. If you attached a weight to the
lower end of the suspended spring how would this affect the oucomes?
Surprisingly, it doesn't. The suspended weight still doesn't begin to
fall until the compression pulse reaches it.
Related experiment: INVISIBLE THWACK.
SOAP BUBBLES AND SOAP FILMS. [Dick and Rae] This recipe is from Richard B.
Minnix and D. Rae Carpenter. Use Joy diswashing liquid (no other brands work
as well). 140cc Joy, 300cc glycerine, and 450cc water. Approximately 1:2:3
ratios. Let the solution age a week before use for best results!
SODA-STRAW WHISTLE. [MG, DES] If you can still find paper soda straws,
try this. Flatten one end. Snip off the edges of that end to form two free
flaps of paper. Blow in that end. The paper acts like the double reed of an oboe.
Flatten the flaps more (or less) as necessary to produce the sound. Different
lengths give different pitch. Start with a long one, and snip off lengths
with scissors, making it successively shorter. When it gets shorter than
an inch or so, be careful not to snip your nose with the scissors.
Find another slightly larger diameter straw to slip over the first to make
a slide-whistle. Cut two to such a length that when played together you hear
beats. Mark one in advance with the proper lengths so you can cut successively
at the marks and produce a perfect ascending scale. Cut several, properly
tuned, to play a simple tune. The opening of "Jingle Bells" requires only
three.
We farm boys used to make goose-feather whistles.
Snip off and discard the portion with the feathers, leaving only about a
two inch piece. Make a diagonal cut at the closed end, raising up a portion
of the shank so it looks like a miniature clarinet mouthpiece. Blow into
it for a high-pitched sound. It can be concealed in the mouth. Also, its
length can be extended with a soda straw or other tube.
SPECTRUM FROM A BALL POINT PEN. Some brands of ball-point pen have a clear
plastic barrel with hexagonal cross section. Pilot © pens do. When these
catch the sunlight they cast a nice spectrum, since the angle between alternate
facets is 60°. You don't need to remove the ink tube from the pen.
Save these pens for lab use. [DES]
Such a pen may also be used in the classroom with an overhead projector.
Mask off all but a narrow 1mm slit on the projector light table. Notice that
only a narrow strip (1 or 2 cm wide) of the projection lens has light passing
through it. Place the pen in this strip of light (and parallel to it)near
the projector lens, and adjust it so that the spectrum it produces is at
minimum deviation. Narrow the slit if necessary to get purer colors. [DES]
Of course a long prism, or diffraction grating, or holographic diffraction
grating can be used with the overhead projector to produce a spectrum, but
the ball-point pen is far less expensive and the result is very good. [DES]
Question 1: Why does this spectrum form a curved rainbow-like arc
on the wall? The answer to this has no connection whatever to the
fact that a rainbow is curved in the sky.
More questions: As you rotate the pen, the spectrum moves through
different angles of deviation from the unaltered beam from the projector.
But there's a distinct position where the deviation is least, called the
minimum deviation angle. Why is this? When the spectrum is at minimum
deviation, the light rays pass through the prism symmetrically, making equal
incident and emergent angles. Why? Why is the dispersion (spread of colors)
greater when the deviation is larger than minimum? What has this to do with
question 1?
SPECTRUM FROM A PROJECTOR. For classroom demonstration an overhead projector
may be used to cast a large circular spectrum on the ceiling.
Obtain a disposable plastic glass, such as those used for cocktails at parties.
These glasses have sloped sides. Nearly fill it with water. Cut a hole in
an opaque paper just a bit larger than the bottom of the glass, and place
this mask on the easel of the overhead projector, with the glass sitting
in the center of the hole.This arrangement casts a circular rainbow on the
ceiling. The size of the hole in the mask may need adjustment. In some cases
the mask is not needed. Block the light on one side of the plastic glass
to demonstrate that the path of the light is upward at an angle into the
sloping side of the plastic glass, through the water, then out the surface
of the water on the other side of the glass. This is especially effective
in a fully darkened room. If the motor of the projector vibrates the water
surface, the spectrum jiggles beautifully. [DES]
ARISTOTELIAN FALLING BODIES. [DES] Aristotle taught that the "natural motion" of a falling
bodies is to fall equal distances in equal times. He also said that the speed
of fall is proportional to the mass. Is this correct? Can we test it? Bodies
falling in fluid media actually fall with constant speed once they reach
terminal speed. So, at terminal speed a body does fall equal distances in
equal times. This can be demonstrated with ordinary coffee filters from coffee
machines, the paper cups sold for baking muffins, or the small cups used
for candies or party favors. When dropped with closed end down, their motion
is rather stable, and they reach terminal speed very quickly.
BALLOON ENIGMA.
Two balloons, partly inflated, are connected at either end of a tube with
a stopcock. (A pinched-off section of rubber tubing may be used.) One balloon
is inflated more than the other. When air is allowed to pass through the
connecting tube, what happens?
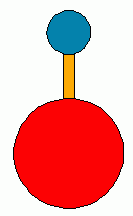If you do
it, and do it successfully, there's a neat joke you can include. Do this
demo with the largest balloon below the other, and say that gravity pulls
air down into it to make it larger.
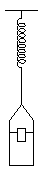BOBBING ON THE WAVES? [BERG] A beaker of water is suspended from a spring. An object
floats in the water. As the beaker-pendulum moves up and down, what happens
to the floating object as the pendulum is at the bottom of its motion. Does
it rise up out of the water, sink deeper, or stay at the same level relative
to the water surface?
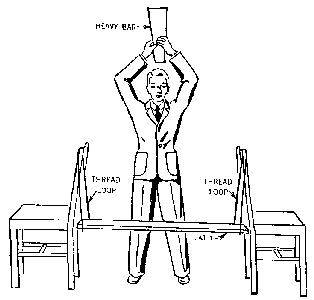BREAK IT.
A wooden slat, or yardstick is suspended by two thread loops, then struck
hard at its center. The wood will break without breaking the strings. The
wood may be suspended from loops of paper held up on razor edges. Pins may
be stuck in the ends of the wood, and the pins supported on the rims of two
wine glasses. Once you convince yourself that very little impulse reaches
the supports before the stick halves drop, you realize that the stick may
be suspended from loops around the ears of two students, without any "Vincent
van Gogh" outcomes. Carnival performers used to do this with the stick suspended
from their eyelids.
Brick structures have very little resistance to being pulled apart at the
mortar lines. Poured-concrete chimneys, especially if they have steel reinforcing
bars, would behave differently under these conditions of demolition.
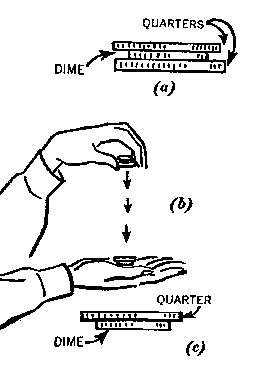COIN DROP.
Hold two quarters and a nickel as shown, between thumb and forefinger. Release
pressure slowly, allowing the bottom two coins to drop. The quarter will
land on top of the nickel if the distance of drop is correct. Practice to
find that distance. Why do the two coins usually turn over as they fall? See also buttered toast.
[Answer]
COMING AND GOING. Weld two semicircular steel rods together and weld or fasten a heavy
ball at each end. Paint the balls different colors, say red and green. At
the center you need something like a ball bearing to allow it to rotate with very small friction with respect to the flat plate that will be placed on your head. When wearing it you'll look like a space alien (see picture). Then when you turn and walk.
The balls keep the same orientation in space. This comes close to being a
pure demonstration of static inertia. [Many demonstrations that claim to demonstrate inertia actually are not so clear-cut, having complicating features.]
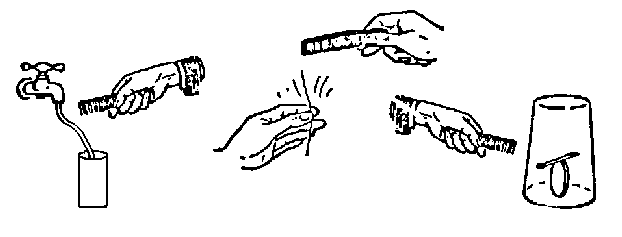
FOOL'S TACKLE.
[DES] The figure shows a pulley arrangement called the "Fool's Tackle", for
only a fool would expect it to work. However, if the diagram is shown to
students (without the forces included) you can ask them what force would
be required to lift the load from the table: W, W/2, W/3, W/4, where W is
the weight of the load.
CTVREO — has magnitude and direction
DSEPE — magnitude portion of velocity
OHNTPO — elementary light wave
[In this, and the following demos using a rotating platform,
consider the policy of your school before letting students do them. It's
not unreasonable to have wrestling-mat pads surrounding the platform, and
have the platform surface padded as well. People become dizzy and have been
known to fall off the seat or platform.]
HIGH ROAD AND
LOW ROAD. [BERG] Two balls are propelled with equal velocity on two tracks.
The tracks start out on the same level, but one has a smooth drop to lower
level, then a rise to higher level. The total length is over a meter. Some
care must be taken to ensure equal firing speeds.
Construction set model. The balls are posing at rest for the photo.
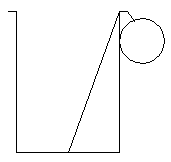INERTIA (BALL
IN CUP). Attach a ball to the bottom of a cup with an elastic band. When
the cup is dropped, what will happen to the ball? Will it stay outside the
cup? Will it jump inside the cup?
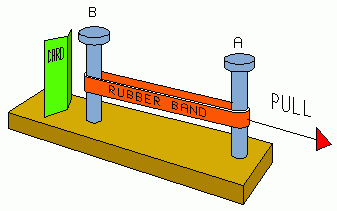
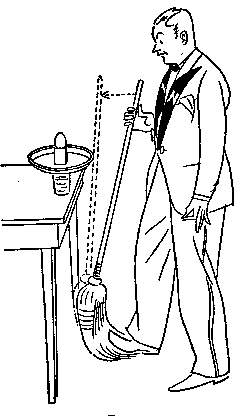
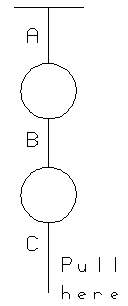JERK. Two
heavy balls are suspended one above the other by strings. When you give a
steady pull on the lower string, C, which string will break?
[Caution: your hand must get out of the way quickly so it
won't be hit by a heavy falling ball. Some demonstrators fasten the lower
string to the center of a wooden dowel, then use both hands on the dowel
ends to jerk it down.]
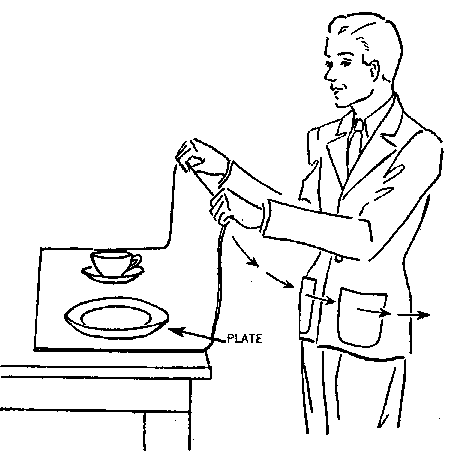
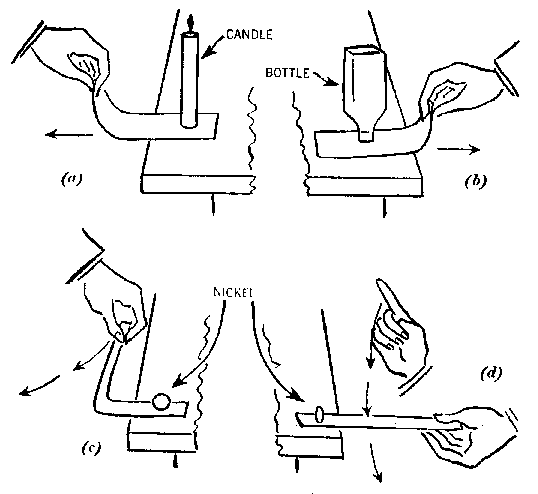
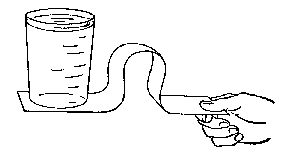These impulse
demos can also be done using a strip of paper and one object, if you haven't
yet acquired a table setting and a silk or rayon cloth. An 8.5 x 11 inch
piece of paper will do. Place it under a beaker or glass of water. Pull slowly.
The glass moves along with the paper. Pull it nearly to the edge of the table.
With the glass in this precipitous position, say "I will now pull the paper
from under the beaker without spilling any water." (Say "pull" not "yank".)
Suspense! Then yank the paper. Follow up by using an empty plastic glass
and show that if the paper isn't pulled quickly enough, the glass will
topple. Practice first.
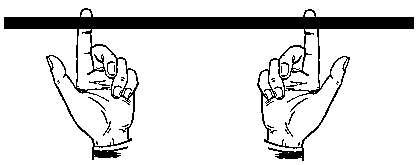LOCATING
THE CENTER OF GRAVITY. Start with your hands outstretched and palms facing
each other about a meter apart. Rest a horizontal stick, cane or metal pipe
on the index fingers of each hand. With your eyes blindfolded, slowly move
your hands together until the palms meet. Regardless of the starting position
of your hands, the center of gravity of the stick will be at the point where
your hands come together. [HG]
The figure
shows that a pair of plane mirrors at right angles behaves differently than
does a single plane mirror. Have two mirrors hinged (for ease of storage)
with a precise arrangement to hold them at perfect right angle alignment
for the demo. Curved cylindrical mirrors can be made by forcing plastic mirrors
into a slight curve. This may not seem like physics, but it is certainly
a good exercise in three-dimensional thinking.
OSCILLATING BEAM. [K&K] A heavy uniform bar or beam rests on top of two identical
rollers that are continuously turned in opposite directions, as shown. There's
friction between the rollers and the bar, and it's constant, independent
of the relative speed of the surfaces. Find the motion of the bar.
[Answer]
Steel construction set model of the oscillating beam. 
PAPER WEIGHT.
The usual demonstration: Cover a thin wooden slat or shingle with
a sheet of newspaper except for a few inches of the slat that project beyond the edge
of the table. Hit the protruding part of the slat with a sharp downward blow
of a sturdy broomstick. The slat breaks without tearing the paper. [HG]
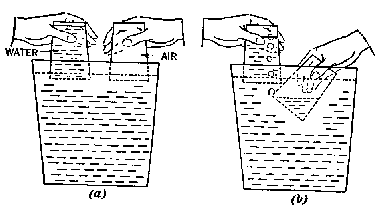POURING AIR.
Submerge a beaker full of water in a large water filled container or fish
tank. Invert the beaker so its open end is down. Invert a second beaker and
submerge it so that air is trapped inside. Pour air from one beaker into
another, pouring up. Note the fluid behavior of the gas. [HG]
RADIOMETER.
The little toys with four metal vanes inside an evacuated glass globe are
readily available. They are sometimes called "light-mills", but the proper
name is "Crookes Radiometer." Many books give incorrect explanations of how
these work, and the correct explanation may be more than you wish to deal
with. Before you demonstrate one, read Bill
Beaty's How does
a light-mill work?.
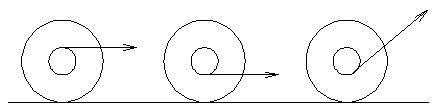PULLING SPOOL.
Select a large spool and wrap several turns of ribbon or cord around it.
Place the spool on a table so it can roll when the free end of the ribbon
is pulled out from the spool bottom. Observe the direction that the spool
rolls when the ribbon is pulled straight up and when it is pulled at other
angles closer to the horizontal. With a little practice, the spool can be
made to roll in either direction as the ribbon angle is changed. Encourage
students to explain the phenomena using terms such as torque, friction, and
vector direction of force. [HG]
At a particular
angle of pull the spool slides without rolling, if the angle is maintained
as it moves. Ask students to determine, from physics principles (forces and
torques), precisely how that angle can be predicted from the nature of the
spool. Answer: The angle is such that a line extended along the ribbon passes
exactly through the point of contact of the spool with the table, therefore
the ribbon exerts no torque about that point. The force due to friction and
the gravitational force mg also pass through that point, so the net
torque about that point is zero, and no rotation can occur around that point.
SELECTIVE IMAGE
INVERSION. Print with capital letters the word TITANIUM DIOXIDE. Use a red
pencil for the first word and a blue pencil for the second. View both words
through the side of a test tube filled with water. Only the red word looks
inverted. [HG]
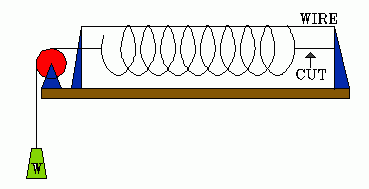Some students
think this has something to do with gravity, or with the non-linear stretch
of the Slinky. Not so. The same Slinky spring can be strung over a taut
horizontal wire or strong nylon cord (about 3 meters long for a plastic Slinky.
A weight (W) attached to one end hangs over a pulley. The other end is pulled
to stretch the Slinky, holding the weight in equilibrium. That end is released.
The weight does not begin to fall immediately, but only when the Slinky is
nearly collapsed. (The end may be attached to a string, which is then cut.)
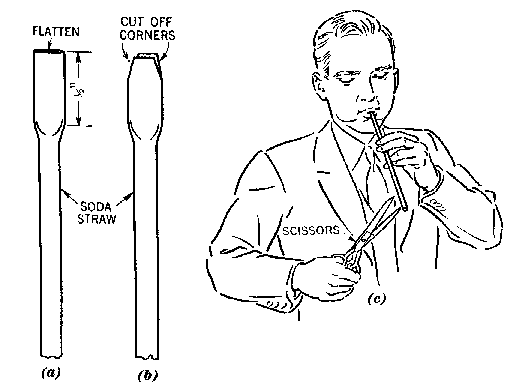
SPECTRUM FROM
A BOWL OF WATER. Submerge a mirror in a bowl of water as shown. When sunlight
falls on the water surface at a low angle, a spectrum will be cast on the
ceiling. Place this near a sunny window of the classroom. [MG]
 |
| Spectrum from light reflected by a needle. From Laboratory Experiments in Practical Physics, Macmillan, 1927. |
|---|
SPECTRUM OF THE SUN. Obviously, looking at the sun with unprotected eyes can be very dangerous. But here's a way the solar spectrum may be observed safely. Place a metal knitting neele, sewing needle, or polished straight metal wire, in the sunlight. With your back to the sun, look at the reflected sunlight from the needle through a prism whose axis is parallel to the wire. The sunlight reflected from the wire (acting as a cylindrical mirror) looks like a very narrow line and performs as a very narrow slit. But it spreads the reflected light so its intensity is low enough to be safe to look at.
A diffraction grating may be used in place of the prism. If you place the needle on the top of an open cardboard box, you can arrange things so that the spectrum is seen against the shaded inside of the box, for better visibility of the colors. Some of the Fraunhoffer dark absorption lines may be observed in the spectrum if you use a prism or grating of high optical quality. The prisms sold in science stores are usually not good enough.
I've seen this demo in older books. For example, Henry Black, Laboratory Experiments in Practical Physics. Macmillan, 1927, p. 227. The needle method was obviously well-known then, but I've not seen it in modern books.
More about this, with spectrum photos.
SPINNING HAMMER. Mark the center of gravity of a hammer with a spot of paint. Toss the hammer into the air with a spin and note that the spot is the most stationary point of the hammer as it spins. Note also that the paint spot moves in a smooth (not wobbly) path, in fact, its path is a parabola.[HG]
Footnote: Is the path of a projectile a parabola, or an ellipse. Isn't a projectile just a body in orbit around the center of the earth? Aren't such orbits always ellipses? [Answer]
SPOOKY BALANCE. Find a large cylindrical object, about 10 or more inches in diameter, and secure it onto a base so it doesn't roll or move. You can easily balance a textbook on it. If one end of the book is pushed down a bit, the book restores to its original position. It can even be placed offside a bit, and it still balances, though tilted. Try wooden blocks of various size and height. Try a stack of blocks, or books. If the height is too great, balance can't be achieved. What determines the maximum height? Note, there must be sufficient friction to allow the balanced object to roll a bit without slipping. But even with large friction (felt on felt) when the height of the balanced object is too great, it won't stay in place. See Kleppner and Kolenkow, problem 6.35. [Answer]
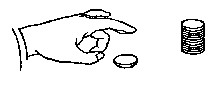STACKED CHIPS.
Stack coins or smooth plastic disks, then aim another coin at the stack.
It will knock out the bottom coin, leaving the stack undisturbed. A thin
ruler, less than the thickness of a coin, may be used to knock out the bottom
coin. Stack alternating colors of chips; swing the ruler back and forth,
separating the two colors of chips.
STANDING WAVES ON A STRING. Wave motion and standing waves can be demonstrated by attaching a vertical string to almost any small electric motor or vibrator. An electric shaver is ideal. Hang weights of varying amounts on the string. As the tension increases, there will be changes in the length of the standing waves. [HG]
UNLIMITED WATER SUPPLY. Suspend a water faucet above a sink by thin wires. Water can be made to flow continuously in a strong stream from the faucet bottom despite the fact that the faucet is not connected to any water pipes. The secret is to use a concealed electric water pump that pushes water up a glass tube into the bottom of the faucet. As the water emerges, it flows over the outside of the glass tube concealing the tube from view. This makes an interesting corridor display. [HG]
STEREOSCOPIC
VISION. Look through a paper tube at some distant object with the right eye
while holding a book over the other eye and close to the tube. It will appear
that one is looking through a hole in the book. [HG] Or, as shown in the
figure, hold up your hand and it will appear that you have a hole in your
hand.
STRETCH CHARGE. Stretch a rubber band tightly and rub it against an electroscope. Determine the nature of the charge produced. [HG]
SUSPENDING SOAP BUBBLES. Show that a soap bubble filled with air will float on carbon dioxide. Using a bubble pipe or straw, blow a soap bubble and carefully place it in the center of a jar partially filled with carbon dioxide. Because the carbon dioxide is invisible the bubble appears to be suspended without any support. [HG]
THUNDER BUBBLES. [Demonstrator and observers should use ear protection.] Prepare a soap bubble solution in a shallow dish or pan. Fill a balloon or beach ball with a 2 to 1 mixture of hydrogen and oxygen. Using a small nozzle delivery tube, blow the gas mixture from the balloon through the soap solution to produce copious bubbles.Pick up handful of bubbles and hold them far out in front of you. Ignite the bubbles with a match. The explosion will not be felt by you. However, someone standing too close to the bubbles may have an ear injured. The sound is indeed intense. Try this in a long hallway for good reverberation. [HG]
THUNDERING GRADUATE. Suspend a coiled platinum wire just below the lip and inside an English graduate containing a few milliliters of ammonium hydroxide (concentrated). Bubble oxygen through the ammonium hydroxide. Violent explosions occur. [HG] Herb, I don't even know what an English graduate is! A metric graduated cylinder would surely work as well here. But I know that an ungraduated cylinder is one that flunked out of school. [DES]
TUBELESS TELEVISION. Prepare a slide for a projector with a few simple words such as "THAT'S ALL, FOLKS" cut into a piece of metal foil and mounted in a glass or cardboard slide. Aim the slide projector so the beam goes from a dakened room, out an open door and does not attract attention. Focus it so that the image of the slide is in an open place, not focused on walls or funiture (or a screen). In the darkened room, wave a white wand in the plane where the image is focused. Persistence of vision creates a complete image, apparently materializing the words in open space. Of course, a magician's "magic" wand works best. [HG]
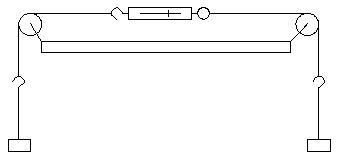TUG OF WAR.
Use two equal weights, suitable for hanging from a cord. Weigh each with
a spring balance to convince students that they have the same weight,
W. Arrange the weights and the spring balance as shown, by hanging
the two weights on strings passing over pulleys to either end of the balance.
Ask students to predict the reading of the balance. Suggest options: 0,
W, W/2, 2W, 3W. You may think this isn't worth the trouble to set up.
But if you do, you may be surprised/dismayed at how many students predict
0 or 2W, or even W/2.
VARIABLE DENSITY. Moth balls rolled in sodium bicarbonate and put into a cylinder of very dilute hydrochloric acid will rise and fall with regularity. [HG]
VARIABLE VOLUME SPONGE. A dry plastic sponge can be measured for volume. Ask how much water you can pick up with it. When wet, it may pick up more than its initial volume. It expands slightly and is mostly a "lot of air holes fastened together." [HG]
VISCOSITY REACTIONS. Let a few students with egg beaters beat oils of different viscosity. Those having to beat the heaviest oils will tire first. [HG]
VISUALIZED WORK UNITS. Mount a 1 foot inch length of 2x2 inch wood upright on a base. Mount another one slightly under 9 inches (0.738 × 12" = 8.85") long on the same base. Lifting a one-pound weight from the base to the top of the one foot tower represents one foot-pound of work. Lifting the weight to the top of the 8.85" tower represents one joule of work.A feather lifted from the table top on to a piece of paper laying on the table represents an erg of work. A millionth of a millionth of an erg is called an electron-volt. [HG]
WATER GLASS SUCKER. Carry a glass brim-full of water up a ladder and press it to the ceiling. Ask the "sucker" to push against the bottom of the glass with a long pole while you climb down and put away the ladder and go on about other business. If the ceiling is smooth, the student need not fear that the glass will fall. [HG]
WATER GLASS PRANK. This is an old restaurant prank. Cover a brimful glass of water with a thin card (such as the restaurant menu).Carefully invert it on a smooth table top, then pull out the card. Leave it for that surly or snobbish waiter or waitress at the greasy spoon diner. Better yet, include the tip (in coins) in the glass first. The clever waitress will know what to do to retrieve the tip without spilling water all over the table and floor. Do you? [DES] [Answer]
WHISTLE BEATS. Prepare two small whistles with a screw in the end so that the length of the air column can be adjusted for different frequencies. Attach the whistles to a Y tube so that they can be blown simultaneously. When the pitch of one is slightly different than the other, a low pitch "beat note" is heard. [HG]
WHISTLE DIFFERENCE TONES. Small and inexpensive double (and sometimes triple) plastic whistles are sold in museum shops, toy stores, science stores, and places where novelties are sold. They have two or three whistles side-by-side so they can be blown simultaneously. The large (foot-long) wooden whistles simulating locomotive whistles are also made this way, with two or more inner chambers of different length. They produce difference tones, equal to the difference of frequency between the pipes, but in the aubible range. (Beats are in the subaudible range.) This is a result of non-linear mixing of the turbulent air near the fipples of the pipes, which are close enough together to allow this. If one cut such a whistle, physically separating the pipes, the difference tone would not be heard when they are blown simultaneously. [DES]
WOOD'S METAL. Carve a spoon mold in wood and fill the mold with molten Wood's metal. The spoon will melt in hot water, coffee, or tea. Save the mold to recast the spoon as part of the demonstration. [HG]
Wood's metal melts at 65.5° Celsius. It may be made by melting together 4 parts by weight of bismuth, 2 parts lead, 1 part tin, and 1 part cadmium. It can be purchased from various web stores.[Sutton, p. 208]
Presentation idea: Casually use the spoon to stir your coffee. Remove it and the bowl is gone. Remark that the coffee is really strong today.
Some Answers
This section is continually under construction. Watch for potholes.
I've received many inquiries (a couple or three, at least) asking "What's that guy doing in the lead illustration of your demo document?" The illustration is from p. 161 of Hopkins' book Experimental Science (1890). It's caption is "Reflection of Light and Sound." Oddly, it isn't specifically explained in the text, but may have been in the issue of Scientific American from which it was taken. As near as I can figure, the sound of the ticking watch at E is reflected from mirror B to mirror A and then focused at C and conducted to the ear through the tube. The flame at the focus of the left mirror illustrates that the mirrors reflect the light in the same manner, back to illuminate the face of the watch. It could also be demonstrating the effect of the focused sound wave on the flame. Anyway, I think it appropriate to illustrate the spirit of physics demonstrations, and the fact that the audience doesn't always know exactly what the demonstrator is doing.
ARISTOTELIAN FALLING BODIES. At terminal speed the drag force on the body is equal in size to the force due to gravity, Fdrag = mg. If the drag is proportional to some power of the speed, say the second power, Fdrag = kv2, and the body reaches terminal speed quickly, then the distance of fall will be approximately d = vt. Let's find the ratio of distances two objects of different mass will fall.
So, d2/d1 = (F2/F1)1/2 = (m2/m1)1/2.
Then if the mass ratio is 4, the distance ratio is 2. If the mass ratio is 2, the distance ratio is 1.414. These may be tested by holding the two objects at heights in these ratios and releasing them simultaneously. They will plop on the floor simultaneously, much to the surprise of students. [<]
COIN DROP. The requirement of retaining the top quarter prevents you from releasing the coins quickly. One edge of the quarter drags on one finger, initiating the flip-over. Try it with a single quarter, nickel, or dime, and tally the statistics. [<]
BUTTERED TOAST. This version of the buttered toast conundrum assumes that the toast slide is butter side up on a table of the usual height, then pushed gently over the table edge. The toast will begin rotation while one edge is still on the table edge, and continue that rotation all the way down. The moment of inertia of the toast about its rotation axis ensures that it will complete a half rotation in the time it takes to reach the floor. If it were dropped from twice that height it would complete a full rotation. The outcome has nothing to do with the toast being heavier on the buttered side. You can test this, if you are willing to clean up the mess, with a toast slice that begins its fall with buttered side down. It should land butter side up. Remember, in all cases to slide the toast off the table top. Don't just drop it from table height by hand. [<]
FALLING LEAKY BUCKET. After the container leaves your hand, moving downward, it is in "free fall" with an acceleration g. The pressure on the water inside is the same everywhere: atmospheric pressure. So there's no pressure difference across the hole to push water out. The leak stops.
The case of upward motion is especially instructive. After the container leaves your hand, moving upward, it is again in "free fall" and has acceleration g, the same as if the cup were falling downward. So, again, there is no pressure difference across the hole and the water flow through the hole stops. During the time your hand was in contact with it, while throwing, accelerating it upward, the water pressures inside are larger than when the container was at rest, and the leak velocity is larger. You could hold your finger over the hole while tossing the bottle upward. During the entire motion up, then down, the acceleration of the bottle and its contents has the same value and the same direction (downward), and that includes the very top of its trajectory. Now if it were spinning, it would have an angular acceleration, and then you would observe leaking water. [<]
FINGER FRINGES. With a point or very fine line source you could see colored diffraction patterns in this situation. But not with a broad source of incoherent light. The fringes seen here are an artifact of our vision. The receptors in our eyes, along with our brain, processes signals to detect contrast and therefore emphasize edges. This causes fringes to be seen around solid objects.See Robert P. Bauman "Diffraction and Non-Diffraction Fringes" The Physics Teacher 34 p. 339 (Sept 1996). [DES] [<]
HEAVY FINGER. This demo is rich in educational value if the details are discussed. Have a student immerse a finger into the beaker. Grill the student to describe what is felt. Most likely the student will simply report feeling pressure. (Some books will try to tell you that an upward force can be felt, but that's too much to expect of our rudimentary sense impressions.) So we need to ask what's the source of the pressure. It is due to forces the water exerts on the finger, and some of those forces have upward components. "Aha!" you say. "What does Newton say about this?" Answer: If the water exerts a force upward on the finger, the finger exerts a downward force on the water.
"But doesn't the water, being fluid, just move aside to accommodate your finger? How does the balance pan know you've put a finger in?"
Answer 1: The water, after insertion of the finger, is in equilibrium, so the net force on the water is zero. The forces on the water from the sides of the beaker add to zero by symmetry. The force of the atmosphere on the water surface is essentially unchanged, except that the surface area is reduced by the inserted finger. But that must be a smaller effect, for it is in the wrong direction to account for the observed result. So if the finger exerts a downward force on the water, the bottom of the beaker must exert an equal size upward force on the water. And if so, the water exerts a downward force on the bottom of the beaker, etc., accounting for the extra force on the pan that pushes it down. But still, there's the nagging question of how, in colloquial terms, "The force of the finger is communicated to the bottom of the beaker." Point out that this language is rather loose, and we seek a better and more detailed answer.
Answer 2: Have a graduated cylinder of water nearby on the table. Push a finger into it. Note that the water level rises. "What does that rise of the water level do? It increases the pressure on the bottom, for that pressure is due to the weight of a column of water supported by the bottom, and we have increased the height of that column of water. This is what happened in the original experiment, but we may not have noticed the water level rise." Do the original experiment again, so everyone does notice. [<]
HIGH ROAD AND LOW ROAD. The balls are neck and neck as the first inclined drop is reached.
The ball that takes the low track attains a greater kinetic energy than
that of the ball on the high path by amount mgh, where h is the height difference
between the level paths. As the low ball enters the level portion of track,
it is already ahead of the high ball because of the speed it gained on its
downward incline, which increases its horizontal component of velocity. The
low ball continues to get farther ahead of the high ball because of its greater
speed. The low ball then loses an amount of kinetic energy on the upward
incline equal to the energy it gained on the downward incline, but when the
two balls are at the same level exiting the track, they have the same kinetic
energy and the same speed. So, is the low ball still ahead of the other one
on exit?
The low ball was ahead of the high ball as it entered the upward incline, and had greater speed, kinetic energy, and momentum. Most importantly, the low ball's kinetic energy was greater than the high ball's kinetic energy by amount mgh (where h is the height difference), and by the time it rises to the height of the upper ball, the two balls again have the same kinetic energy, and the same speed. But the ball that traveled the low track got sufficiently ahead of the other one that it is still ahead when they exit the apparatus.
Perceptive readers will realize that this outcome depends on the lower horizontal track being long enough for the lower ball to get sufficiently far enough ahead of the other one that even with its loss of speed climbing the ramp, it is still ahead on exit. Try it with shorter tracks. We have ignored slowing of both balls due to friction and rolling resistance, treating these effects as comparable for both balls, any difference having negligible effect on the outcome, but in the real apparatus this might not be so. You can satisfy your concerns about this by doing experimental tinkering with the apparatus. That's why the steel construction set apparatus is ideal. We have also neglected rotational energy and momentum. Tsk! Tsk! The purpose of this demonstration is to convince students that superficial, naive and common sense expectations can be seriously wrong. Therefore it is important to observe and carefully consider the details, using basic physical laws. Also, it shows the importance of hands-on physics experience. [<]
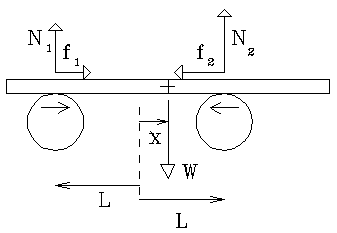OSCILLATING
BEAM. The forces on the beam are shown. The centers of the wheels are each
a distance L from the centerline (dotted) of the apparatus. The friction
forces are in opposite directions:
f1 = μN1 and f2 = μN2
Take torques about the center of mass of the beam, shown by the + symbol in the diagram.
-Wx - N1L + N2L = 0
Then: Wx/L = N1 - N2
The net force on the beam is F = f1 - f2 = μ(N1 - N2)
So,-Wx/L = (f1 - f2)/μ
F = f1 - f2 = -μxW/L = -(μW/L)x = ma
So the acceleration of the beam is proportional to the negative of its displacement, and therefore its motion is simple harmonic. So what happens if both wheels turn the other direction? The friction forces change sign, and we get the result +(μW/L)x = ma, which tells us the acceleration of the beam increases with displacement, so the slightest displacement increases till the beam moves off the wheels. [<]
ROLLING SPOOL. The demonstration of the cylinder sliding without rolling on a horizontal surface is a cheat, but a subtle one. I use a roll of cash register paper, and pulled slowly. The weight of the roll crushes the paper beneath it, making it slightly thinner. So the spool rides on a shallow depression in the paper. The paper exerts a force on the spool that isn't exactly normal, but is tilted slightly in the backward direction (opposite to the motion). This off-normal force provides a torque of equal size and opposite direction to the torque due to friction. The force due to friction is mainly responsible for the forward motion, reduced slightly by the small backward horizontal component of the off-normal force.
To ensure that it works every time you can "cheat" by piling weights on the roll for a while as it lays on its side, producing two flattened regions. Of course we physicists would never cheat, would we? A simpler insurance trick is to put a short steel or lead rod in the center of the spool.
This geometry of forces and torques on the spool is similar to that responsible for rolling resistance. [<]
SPOOKY BALANCE.
Let H be the distance from the bottom of the balanced object and its center
of mass, measured perpendicular from the bottom surface. M is its mass. When
the balanced object is disturbed, it can roll without slipping to a position
tilted at angle β. The point of contact has moved through the same
angle with respect to the center of the cylinder, and through an arc of length
Rβ, where R is the radius of the cylinder. The block is stable if the
line of action of Mg falls within Rβ of center, so Mg
produces a restoring
torque. The block is unstable if (H/2) tanβ > Rβ. For
small angles β, tanβ is approximately equal to
β, therefore the block is unstable if H > 2R. [K&K,
problem 6.35] [<]
TRAJECTORIES. The paths of projectiles near the earth's surfaces (ignoring air drag) are portions of ellipses, as are any periodic orbits, such as that of the moon around the earth, or artificial earth satellites. The projectile's elliptical path, if extended, would pass through the volume of the earth, and the center of the earth would be at one of its foci. Then why do measurements of height and range of projectiles obey equations that describe parabolas?
 |
| Transofrming an ellipse to a parabloa. |
|---|
y = voy + (1/2)at2
x = voxt
Here y is height above the earth's surface and x is distance along the earth's surface. We may graph these on cartesian paper, but that's not quite fair. Heights are actually radial lines from the center of the earth, and aren't parallel, but divergent. Distances along the earth's surface aren't straight, but are circular arcs. They should be graphed on polar coordinate paper. When you do this correctly on polar coordinate paper, the path is a segment of an ellipse. When graphed on cartesian paper it is a segment of a parabola. When a parabola on cartesian paper is mapped onto polar coordinate paper it becomes an ellipse. And vice versa. Isn't that remarkable! Can the mathematically inclined among you prove this?
A textbook asks, "Is the path of a trajectory an ellipse, or a parabola?" What's the answer? Actually textbooks shouldn't ask such dumb questions. Here's two pictures. One is of a parabola, one is of an ellipse. Can you tell which is which?
 |
 |
 |
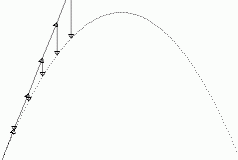| Trajectory with and without air drag. |
|---|
Answer: The ellipse is on the left, the parabola on the right. When only part of either curve is shown, the differences are negligible. In fact, if we take air drag into account, the resulting curve is also hardly distinguishable from these. This figure shows a trajectory without drag (solid) and a trajectory with air drag (dotted). The range is shorter, but the distance to the highest point is also shorter. Either one would "fit" the mathematical form of an ellipse, or of a parabola, to within the usual experimental error. See how textbooks deceive?
The culprit here is the use of "is" in the question. This is one of those dangerous words in science. Another dangerous word is "because".
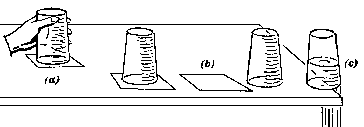WATER GLASS
PRANK. Slide the glass to the edge of the table, and catch the water in a
container below the edge of the table. It's also possible to insert a thin
card (or menu) under the inverted water glass without losing much water.
Then invert the glass. [<]
w
Sources, contributors and additional references
- Anon. Social Tricks for Entertaining. No author listed. Illinois Herb Co. (1930s?)
- Arons, Arnold B. Teaching Introductory Physics. Wiley, 1997. This is an essential resource for the physics teacher who wants to "get it right." [Arons]
- Berg, Richard. University of Maryland, from his Physics IQ Test demo show. [BERG]
- Black, Henry. Laboratory Experiments in Practical Physics. Macmillan, 1927.
- Brown, Bob. Science Treasures, How to Repeat the Great Experiments. Cornerstone Library, 1969.
- Carpenter, D. Rae Jr., and Richard B. Minnix. The Dick and Rae Physics Demo Handbook. Dick and Rae, Inc., 1993. Dick and Rae are from Virginia Military Institute. I haven't seen their book, but have seen their shows. [Dick and Rae]
- Ehrlich, Robert. Why Toast Lands Jelly-Side Down, Zen and the Art of Physics Demonstrations. Princeton University Press, 1997. I discovered this book after I'd begun this web page, and reading it made me wonder why I bothered. It is one of the few demo books that explains the underlying physics, with mathematical analysis. Better yet, Ehrlich shares my opinion that simple apparatus is best, and that demos aren't worth doing unless you are willing to examine all of the details with a class. [Ehrlich, Toast]
- Ehrlich, Robert. Turning the World Inside Out and 174 Other Simple Physics Demonstrations. Princeton University Press, 1990. [Ehrlich, World]
- Everett, J. D. Deschanel's Natural Philosophy. Appleton and Company, 1873. Out of print. Another good source of old engravings.
- Frank, J. O. and Guy J. Barlow. Mystery Experiments and Problems for Science Classes and Science Clubs. J. O. Frank & Sons, 1934.
- Frier, George D. University Physics. Meredith, 1965. A physics textbook with marginal notes including pictures and brief descriptions of suitable demonstrations for the concepts being discussed.
- Frier, George D. and Frances J. Anderson. A Demonstration Handbook for Physics. 1972, 1978, reprinted by American Institute of Physics, 1981.
- Gardner, Martin. Various sources and his personal files. See also his "Physics Trick of the Month" contributions to The Physics Teacher. [MG-PT]
- Gardner, Martin. Science Puzzlers. Scholastic Book Services, 1960. Republished as Entertaining Science Experiments With Everyday Objects Dover, 1981. [MG-SP]
- Gardner, Martin. Encyclopedia of Impromptu Magic. Magic, Inc. 1978, 1985, 1991. [MG-1] Illustrations from this book have been used below, with Mr. Gardner's permission.
- Gardner, Martin. Martin Gardner Presents. Richard Kaufman and Alan Greenberg, 1993. [MG-2]
- Good, Arthur. 100 Amazing Magic Tricks. Translated and Adapted by David Roberts. Pinnacle Books, 1977. Yet another reworking of the 1890 Columbus' Egg materials (see Lanners),
- Hopkins, George M. Experimental Science, Elementary Practical and Experimental Physics. Munn & Co. 1890. Out of print. I hope to use some of the 680 fine engravings from this book here if I'm granted enough disk space.
- Kleppner Daniel and Robert Kolenkow. An Introduction to Mechanics, McGraw-Hill, 1973. Some problems in this book are derived from standard classroom demonstration apparatus or are easily constructed. Several of these are in the collection below. The book has a solutions manual, available to teachers. [K&K]
- Lanners, Edi. Secrets of 123 Old-Time Science Tricks & Experiments. TAB Books, 1981. Original by Verlag C. J. Bucher, Lucerne and Frankfurt, 1976. First English Language Edition by Paddington Press U.K. Ltd., 1978. Translation of Kolumbus-Eier, based on a larger collection entitled Columbus' Egg, first issued by the editors of Der Gute Kamerad in, two volumes, 1890. Most of the illustrations are by Poyet.
- Lynde, Carleton John. Science Experiments with Home Equipment. International Textbook company, 1937, Van Nostrand 1949. [Lynde, 1949]
- Lynde, Carleton John. Science Experiences with Ten-Cent Store Equipment. International Textbook Company, 1941.[Lynde, 1941]
- Meiners, Harry F., Ed. Physics Demonstration Experiments. Two volumes. The Ronald Press Company, 1970.
- van Rensselaer, Alexander. Fun With Stunts. Blaikston, 1945. Reprint of Betcha Can't Do It (1940) and Try This One! (1941).
- Sutton, Richard Manliffe. Demonstration Experiments in Physics. McGraw-Hill, 1938. [Sutton]
- Richard B. Minnix and D. Rae Carpenter. [Dick and Rae.]
- Herb Gottlieb. [HG].
- Donald Simanek. [DES].
Return to Donald Simanek's page.
Since 8/30/01
folks who must see it to believe it have visited this page.
Last revision Feb 2007.