This, like many pages at this site, is a work in progress. Expect revisions
and addition of new material. Since these pages are written in bits and pieces
over a long period of time, there's bound to be some repetition of ideas.
This may be annoying to those who read from beginning to end, and may be
just fine for those who read these pages in bits and pieces.
The Reading Room.
Related Galleries.
Web resources.
- Deceptions by Peter Parsons. We don't talk much about deliberate contemporary scams and deceptions on these pages. We don't have to, for this excellent site debunks them thoroughly. Click on the "scams" tab for more. The site also has information on both genuine and bogus energy saving strategies.
| The seekers after perpetual motion
are trying to get something from nothing.
|
The Main Gallery
It'll never work!
 |
| Closed-cycle mill, 17th century. |
|---|
The term "perpetual motion machine" has several definitions.
- Any device that continues its motion forever, without any speed reduction. This is
a literal interpretation of the words.
- Any device whose operation would violate established laws of physics, or would depend upon purely speculative laws unknown to physics. This is the colloquial usage.
- A machine that perpetually puts out more energy than it takes in. Nowadays this is
called an "over-unity machine" since its power efficiency would be greater than one.
I will include the last two of these under the term "unworkable devices". The first one
does not violate any fundamental physics, but it does not happen in large-scale structures because of two facts of nature: (1) no materials are perfectly rigid bodies and (2) friction and other energy-dissipative processes are always present. The only systems we know of, such as atoms, that seem to exhibit constant energy and momentum forever (if undisturbed) are such a nature that we cannot directly verify whether there's really any motion going on within them. Our concern is not with these, but with systems that would appear to violate physics laws on the macroscopic scale—machines that have cyclic operation and could be made to produce useful work forever, without energy input.
|
The Perpetual Quest
Seekers of Perpetual Motion,
Have fervent faith and saint's devotion.
The Gods of Physics duly smite them
To be reborn ad infinitum.
|
|
Perpetual motion machine proposals are often dismissed by scientists in a manner that
appears to the layperson as hasty rejection using dogmatic assertions that
such machines are prohibited from working by the "laws of thermodynamics".
This does not satisfy the person who "knows" a little physics, but considers
the laws of thermodynamics a bit mysterious. The very character of such laws
is off-putting to the average person, because they have an air of finality
and negativity.
Thermodynamics laws and conservation laws have great power because they allow
us to predict certain things about a system without analyzing all aspects
of the mechanism. They even allow confident predictions in spite of our ignorance
of some details or experimental difficulties in examining them. The experienced
scientist will use these to evaluate a proposed device, which seems to the non-scientist
to be a failure to consider all the details.
Of course physicists don't claim that any physics laws represent final and
unalterable truth. The perpetual motion (PM) machine inventor pounces on
this and says "Such laws would have us give up trying to discover anything
new! What if there were a flaw in these laws, a flaw that we could discover and
exploit?"
|
The only way of discovering the limits of the possible is to venture a little way past them into the impossible.
— Arthur C. Clarke (Clarke's second law) |
|
It's a historical fact that the laws of thermodynamics were initially proposed
to describe the fact that all previous attempts to achieve perpetual motion
had failed. We've learned more about these laws since then, and have a much
better understanding of them and why they are so powerful in describing what
can and can't happen in nature.
Any particular classical mechanical PM machine can be shown to be faulty in concept
or execution by far simpler and conclusive means. The obvious way is to simply test the machine to see if it lives up to the inventor's claims. Fraudulent claims
may sometimes be exposed this way. But the inventor's usual reaction to the failure of his device is to say, "It just needs a bit more work to refine and improve the design or reduce the friction."
On another level are proposals that haven't yet been built. Such
proposals may come from honest (though perhaps misguided) people who know
some physics or engineering (but not enough). How can we determine whether
these are worth the time and trouble to develop? We may not have to go to the
trouble and expense of building them. Perpetual motion proposals can
be shown to be based on faulty reasoning, or on misunderstanding or
misapplication of well-known and well-tested basic laws and principles of
physics.
This can be a useful exercise for interested laypersons, and for high school
and freshman college students taking physics, even before they have been
exposed to the laws of thermodynamics. My purpose, in this document, is to
subject some of the classic perpetual motion machine proposals to such analysis. In the
process we will come to better understand the basic physics laws, and understand
how they can be misunderstood, misinterpreted and misapplied. This exercise can
strengthen one's understanding of physics.
| He is wise who gains wisdom from another's mishaps.
|
|
I will be interested in examining examples of these classes of proposals
and claims:
(1) Devices that are claimed to remain in continual motion without input
of energy and without producing output work. Obviously such devices would require
energy to get them moving, but none thereafter. This description is nothing
more than a statement of what perpetual motion means. These devices (if they actually worked)
would have no purpose other than to amaze onlookers and annoy physicists and engineers.
Such devices would not necessarily violate any fundamental physics laws or principles. Stable
atoms are physical objects whose internal processes continue forever without
loss of energy, if the atom is not disturbed. So they are examples of "perpetual
motion" (moving forever), but in the physics literature these aren't called
"perpetual motion machines". That term is reserved for a device that would
violate one or more of the laws of thermodynamics. This is because the word
"machine" is reserved for devices that produce an output of useful work, while these
continually turning systems don't output any work and therefore aren't machines.
Some folks cite the motion of planets around the sun as an example of perpetual motion. On the macroscopic scale we can show that perpetual motion isn't happening, even without waiting around for an eternity. If the motion of a system is observed for a finite time and found to be decreasing in speed,
then clearly it is losing energy continually, and can't move perpetually. This is the case even
for the solar system, as mechanical energy and tidal deformations dissipate mechanical energy into thermal energy. There are no macroscopic (large scale) mechanisms known that move without slowing down, and it is usually due to those
ever-present energy dissipative processes such as friction. The
fact that these dissipative processes are always present is a fact of nature, though we don't usually
elevate that fact to the status of a "law of nature". This fact, however, is not the sole cause of
failure of all perpetual motion machine proposals, as we will see.
(2) Devices that are claimed to remain in motion without energy input while still
producing output energy. Such proposed devices may require a push to get
them started, but no input energy thereafter. This is the kind of machine
inventors seek. Sometimes the inventor refuses to disconnect the starter
battery after the machine is moving. This is suspicious.
| Human opinion is scarcely anything more than the history of human errors.
|
|
(3) Devices that require energy input to remain in motion, but are claimed
to produce output energy greater than the input energy. These days some folks
call these "over-unity" machines, because their inventors claim they have
energy efficiencies greater than one. Clearly such a machine (if it existed) could
be engineered to be a class (2) machine by simply diverting part of the output
energy and feeding it back to the input to drive the machine. Curiously,
inventors who claim to have made an over-unity machine resist any suggestions
that they do this in order to conclusively prove their claims for the machine.
This is also suspicious.
(4) Devices that tap some hypothetical universal all-pervasive "free energy"
that the inventors imagine fills all of space. Back in the 19th century
it used to be the energy
of the luminiferous ether that was supposedly being tapped. Now that we
no longer take the existence of the ether seriously these folks claim
to be tapping some sort of "energy
of the vacuum." Anyway, they claim, it's "out there" and free for the taking.
If there really were such an energy source, these machines wouldn't be violating
any physical laws. Unfortunately the postulated source of energy is often concocted just
to suit the purposes of the inventor, and is entirely a product of the inventor's
imagination, unsupported by any other independent evidence. So, to the objective
observer, these machines are experimentally and theoretically indistinguishable
from type (3).
Since inventors (seekers) of free energy devices claim that such machines do have
energy input, they reject the label of "perpetual-motion machines". They
also reject any suggestion that they could divert
some output energy to the provide the necessary input, on the excuse that the machines are only
capable of taking in energy from a "free energy" source, or that the "free
energy" is of a subtly different character from ordinary energy.
Scientists classify PM machines by reference to the thermodynamics laws
they would violate.
-
Perpetual motion machines of the first kind violate the first law of thermodynamics. They produce more energy output than input, that is, they have an efficiency greater than one.
-
Perpetual motion machines of the second kind violate the second law of thermodynamics. They would involve zero or negative changes of entropy.
I won't use this classification much, for I want to avoid any appeal to the
laws of thermodynamics in this document. My intent is to show that all unworkable
devices violate more fundamental laws, laws that have been well-tested,
well-established,
and well-integrated into physical theory. Usually these are laws presented in undergraduate
physics textbooks. But the examples I intend to analyze
are those that are given inadequate analysis in standard books and articles.
Many were originally proposed not as workable machines, but as clever challenge
puzzles and paradoxes to test understanding of physical principles.
Top
Overbalanced wheels.
The overbalanced wheel perpetual motion idea apparently originated in India,
in the 8th century CE. In his Sysyadhivrddhida Tantra (748 CE) the Indian astronomer Lalla described a self-rotating wheel driven by mercury moving along its curved spokes.
A variation of this idea was described by the Indian
author Bhaskara (c. 1159). It was a wheel with containers of mercury
around its rim. As the wheel turned, the mercury was supposed to move within
the containers in such a way that the wheel would always be heavier on one
side of the axle. [GIF by Hans-Peter Gramatke, used with permission.]
| Various spellings are seen: "Honecort" and "Honnecort". "Villard" is sometimes seen as "Vilars", "Wilars" or "Willars". | |
This idea appears again in Europe in the year 1235 when the French architect
Villard de Honnecourt described an overbalanced wheel with hinged hammers
equally spaced around its rim. The picture displays ambiguous perspective.
The wheel is actually supposed to be perpendicular to the frame and to the
horizontal axle. Villard's description (translated) is:
Many a time have skilful workmen tried to contrive a wheel that should
turn of itself; here is a way to make such a one, by means of an uneven number
of mallets, or by quicksilver.
The reference to quicksilver (the liquid element mercury) indicates that Villard
was familiar with the Bhaskara device, whose design had reached Europe by way of Arabia. Villard claimed his machine would be useful for sawing wood and
raising weights.
Villard's diagram shows seven hammers, and he insisted
on an odd (uneven) number of hammers, explaining
...there will always be four on the downward side of the wheel and only three on
the upward side; thus the mallet or bag will always fall over to the left
as it reaches the top, ad infinitum.
But, whether the number of hammers is odd or even, such a wheel comes to
rest very soon. You have to give it a forceful push to make it execute even one revolution.
This "overbalanced
wheel" idea reappeared in an astounding variety of forms over the centuries.
We show a better diagram from a later time. A system of pegs or stops was
required to hold the hammers at a large distance from the axle after they
flipped over the top and allow them to hang freely as they came around the
other side. Perhaps the rationale was that the balls had more moment (of
inertia) on one side due to the larger lever arms (even though the principles
of torque hadn't yet been formalized at this time).
Even though there are fewer balls on one side of the axle at any given position,
these have larger lever arms and therefore greater torque. As a hammer swings
and falls near the top of the wheel, the wheel slows during the hammer fall,
then gains some speed when the hammer hits its peg. There's no net gain in
speed, and there's irreversible energy loss when hammers hit pegs. If given
a push, the wheel will turn jerkily for a while. If it were given a very
forceful initial push, the hammers would assume radial positions and the
wheel would turn much more smoothly and efficiently, but would gradually
lose speed and rotational energy because of air drag and bearing friction,
just as any spinning wheel would.
We have mostly second-hand accounts of Villard's understanding of the principles
of this machine. However, I do not think that the folks who were fascinated
with this idea were unaware of the static balance condition of the wheel.
I speculate that they supposed the wheel would only work after it was manually
set in motion, with the hammers giving it extra boost as they rapidly flipped
across the top, perhaps (they may have thought) this was due to some "advantage"
obtained from the motion of each weight flipping to a position with a larger
lever arm.
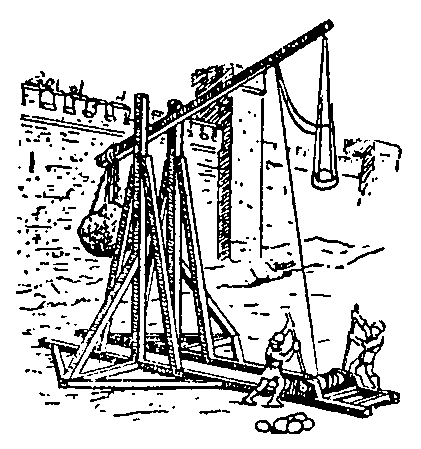This flipping action is much
like that of a sling that gives a person the ability to throw a rock a greater
distance, or the sling siege engine catapult known as the Trebuchet. Honnecort
wrote about these machines of war, describing one with an 8x12x12 foot box
of sand as counterweight (which could weigh 80 tons). Some had arms 50 feet
long and were capable of slinging a 300 pound stone 300 yards. This connection
to the swinging hammers of Honnecort's wheel and Trebuchets is speculation on my part, unsupported by any historical study I've seen.
Even though the sling action of a Trebuchet allows a greater efficiency of
energy conversion compared to the rigid-arm catapult, the machine still puts
out no more energy than that of the falling weight that drives it. Modern
Trebuchets (built by hobbyists) have achieved energy conversion efficiencies
of greater than 65%.
The overbalanced wheel idea was re-invented many times over the centuries,
sometimes in fantastically elaborate variations. None ever worked as
their inventors intended. But hope never dies. I've seen examples made
by country blacksmiths and basement tinkerers. The classical mechanics necessary
to analyze mechanical systems is now well known, and when one takes the trouble
to do this there's no mystery at all why they don't turn forever, and no
reason why they should.
Top
Simon Stevin's problem
 |
 |
| Simon Stevin (1548-1620) |
Stevin's ball-ramp experiment,
the "clootcrans" (chain of balls). |
Flemish mathematician and engineer Simon Stevin (1548-1620) studied the
principles of mechanisms and machines. He was a forceful critic of much of
Aristotle's mechanics; his own studies were more in the Archimedian tradition.
One of Stevin's most acclaimed contributions to mechanics was his use of a
chain of balls (clootcrans) on two inclined ramps as a means for developing
a method of what we would today call the force parallelogram.
Stevin made use of this ball-chain in a creative way. He forthrightly asserted
that any notion that the chain might move of its own accord was obviously absurd. He
gives no reason for this, perhaps assuming that none was necessary. Perhaps
underlying this was the fact that if the chain were to move a distance equal to
the separation of the balls (in either direction), the new position would be
identical to the previous one. In effect, no physical change had occurred, therefore
it won't happen without external influence. If so, this is an early use of what is today
known as the "principle of virtual work", or sometimes "Stevin's principle."
Taking his starting point as the fact that the chain does not move perpetually,
Stevin derived the equivalent of the modern law of composition of forces.
Stevin considered this to be so important that this picture of the ball-chain appears
on the title page of Stevin's book on mechanics, as his "trademark".
Stevin's achievement was an early example of how one can carefully analyze
a mechanical system to determine whether (and how) it works. Stevin accomplished
this long before the vector methods of force analysis were understood, and before formulation of conservation of energy and the laws of thermodynamics. Stevin also adopted the useful tactic of analyzing mechanisms in the "ideal" case where friction is assumed absent.
Some books cite this as Stevin's proof of the impossibility of perpetual motion. That
was not the case, for Stevin simply assumed the impossibility of perpetual motion,
at least in this situation.
Top
More on Stevin's principle
Stevin's principle is useful for problems in equilibrium, and is mathematically
equivalent to force analysis. In a mechanical system where things are free
to move, will they? One way to find out is to mathematically analyze the sum of forces
on each part of the system (and also do the same for torques). If they add to zero, the parts won't accelerate.
Stevin's principle allows us to do this in an alternate (yet equivalent)
way. The method starts by imagining a "virtual displacement" of the system,
then calculate the net work during this "virtual"
motion. This is called the "virtual work". If the net virtual work is zero,
the system is in equilibrium, and will not
accelerate. In practice the analysis is usually carried out by imagining
very small displacements.
[The virtual displacements need not be actual or even likely ones. For example,
to calculate the tension force in a bridge girder, one may imagine the girder
being broken or cut and the pieces that are allowed to move.]
This method is particularly useful for systems that are frictionless or
nearly so. This is ideal for examining perpetual motion machine proposals. It's a Gedanken
(thought) experiment, but when no working model of the machine is supplied,
that's all we have to work with. We imagine the system to be frictionless
(giving the inventor the advantage) then if we can show that even with this
advantage the machine still can't work as claimed, we can consign
the proposal to the Museum of Unworkable Devices.
Before we
return to Stevin's problem of the double ramp and chain let's first consider
the related problem of a double ramp of height z and ramp lengths
x and y. Let's say that x < y. A weight
A is on the x ramp and a weight B is on the
y ramp. They are connected by a rope passing over a pulley at the
top.
Reminder: Work is done on a body when it moves under the action of a force.
Work is the product of the force component in the direction of motion and
the distance the body moves.
Imagine a motion of A up the ramp length x that moves
mass A a vertical distance z. This causes B to
move the same distance x down its ramp, or a fraction x/y
of the length of that ramp, and therefore a vertical distance (x/y)z
down. We conclude that for equilibrium these weights and distances must satisfy
Ay = Bx, or A/B = x/y.
| Be skeptical of any perpetual-motion
proposal in which the assumed motion causes no change in the position of
the center of mass of any part of the system. |
|
Returning to Stevin's problem, using the same ramp, the portion of chain
on ramp x has length x. The portion on y has length
y. The weights of chain are in proportion to the lengths, so A/B
= x/y automatically satisfies the condition for equilibrium. Therefore
the system will not move on its own initiative. The lower loop of chain obviously
contributes nothing that would disturb equilibrium.
The principle of virtual work can be extended to torques, and in modern form
is:
If the virtual work done by all external forces acting on a
particle, a rigid body, or a system of connected rigid bodies with ideal
(frictionless) connections and supports, is zero for all virtual displacements
of the system, then the system is in equilibrium.
Let's not dismiss that lower loop so casually, for it is doing something
very important here. During any virtual (imagined) motion, it is supplying
new mass to the portion of chain lying on one side of the ramp exactly as
fast as the portion of chain on the other side of the ramp loses mass. It
is supplying momentum to one segment of chain at the same rate
as momentum
is lost from the other segment. This, however, does nothing to improve the
PM machine's chances of working. It is a mechanism that keeps the ramp portion
of the system unchanged over time, even during virtual motion. We will see
this process at work (virtual work, of course) in many other perpetual machine
proposals.
We may restate Stevin's principle in a form more directly applicable to devices
claimed to be perpetual motion machines:
If an assumed (virtual) motion of the machine results in a final state of
the system (the machine and its interactive environment) indistinguishable
from its initial state, and zero net work is done on the system during this
motion (no work in; no work out) then that assumed motion will not occur.
Stevin's principle is a particularly appropriate first step in analyzing cyclic and
wheel-type machines where a finite rotation of the wheel changes nothing but its
position. It is particularly useful when analyzing those machines for which the
inventor's initial casual analysis (usually containing a flaw of physics
or reasoning) leads us to think "That machine will surely turn." It immediately discredits the Honnecort wheel and also Stevin's original problem of the ball-chain on ramps. Most
of the textbook examples of Stevin's principle show only cases where the
initial and final states of the system are very obviously different (things
are in different places). But the real power of the principle is that it
can also be applied to cases where the final state "looks just like" the
initial state.
For machines that have a "cyclic" behavior (most do) the analysis must be
carried out over a complete cycle, for energy may be stored during part of
a cycle and released during another part.
Refer back to the double ramp picture. If the chain is imagined to undergo
a virtual motion carrying each ball to the position occupied by the next
one, then the initial and final states are identical. Stevin's principle
then says that the chain will not of itself undergo this motion.
Top.
| Friction is never the only reason why
a perpetual motion machine won't work. Remove the friction and it still won't
work as the inventor intended. |
|
Friction and idealizations.
To assert that a device "Will not work because of friction"
diverts our attention from far more fundamental flaws of the proposal.
Friction is ever-present in nature. Yet, in analyzing PM proposals, it is
useful to assume frictionless components, for in all non-trivial PM proposals,
friction is never the sole problem. Remove all dissipative process such as
friction, use idealized components, and at best the devices will be only
our type (1). They cycle uselessly forever without additional input or output
work.
Frictionless components do not violate fundamental macroscopic principles
of physics. If removal
of all dissipative processes results in a perpetual motion device of type
(1), you know you've probably done the analysis correctly, making no blunders.
But other idealizations do violate fundamental macroscopic classical
physics principles. Remember that we are speaking now of the macroscopic (large scale)
physics processes, not those at the microscopic scale of atoms or smaller.
-
Massless components that are capable of exerting forces on other components
would violate Newton's second law.
-
Components that exert forces without accompanying reaction forces would
violate Newton's third law.
-
Perfectly rigid bodies capable of exerting forces on other such bodies violate
Newton's laws also. All matter can be compressed or stretched, giving rise
to elastic forces. If bodies were perfectly rigid we'd have infinite forces
acting for infinitesimal times. We cannot assume such things in the real
world.
-
A material macroscopic body cannot be observed in two places simultaneously.
-
No information can travel between two separated points instantaneously. This
is another reason why perfectly rigid bodies can't exist. If you pushed on
one end of a perfectly rigid stick, the other end would move instantaneously.
But that's not possible, for it would mean the other end received information about
the push instantaneously.
-
Mass cannot vanish from one place and time and reappear at
another place and time.
Top.
Tapping quantum weirdness
| Nature abhors macroscopic perpetual motion. — D.E.S. |
|
Nature's prohibitions listed in the last section apply to macroscopic (large scale) physical objects. Is it possible that these can be violated on the microscopic (small scale) world of atoms and smaller entities? Certain currently popular speculative theoretical ideas suggest that.
Nature does not prohibit perpetual motion. No laws of nature would be violated by something existing forever in a non-zero energy state. Presumably undisturbed atoms can do that. Whatever is "going on" within an atom continues undiminished forever if the atom is left undisturbed. What nature does seem to prohibit is a system that produces useful work in amount greater than its energy input.
| The perpetual motion machines that
seem to work best are those that turn out to be fraudulent. — D.E.S. |
|
In these pages I have indeed neglected current speculations in physics such as string theory, vacuum energy, black holes, wormholes, dark energy, dark matter, parallel universes, etc. I'm probably not sufficiently knowledgeable about these matters to discuss them effectively. I do note that many of these concepts are "virtual" entities that are part of the mathematical theory, but are not directly observable. And when these do have observable (experimentally measurable) consequences, nature seems to prohibit them being converted to continuous output of useful work on a macroscopic scale. So our hopes of making a macroscopic perpetual motion device based on them is apparently futile. The more we learn about nature, the more evidence we accumulate that "Nature abhors macroscopic perpetual motion."
A very interesting book discussing these matters is "How to Build a Time Machine" by Paul Davies. It is now out in paperback from Penguin Books at $13.00. The cover blurb says "A quick...lucid romp [through] wormholes, naked singularities, alternative universe, cosmic strings, exotic matter, negative energy, imaginary mass, gravitational time dilation, rising entropy and falling information" —San Francisco Chronicle. Davies' book concludes that nature does have taboos: "No time machines, no perpetual motion machines, no naked singularities! Etc."
Top.
| Shouldn't all perpetual motion machines
come with a limited warranty? — D.E.S. |
|
What about "free energy"?
When analyzing PM proposals, one must watch out for "hidden" energy sources.
If the chain of the Stevin machine consisted of interlinked cylindrical rollers,
it might be made to move if there were a small battery and a motor within
each cylinder. Many classic perpetual motion machine scams are done this
way. But in this case, the initial and final states are not identical, for
the state of the batteries changes as power is drawn from them. Some of the
early fraudulent demos of PM machines may well have been driven by hidden
internal stored energy, allowing a massive, well-balanced and low friction
wheel to turn for a very long time before slowing perceptibly.
"Free-energy" enthusiasts claim that if a machine were tapping some invisible
energy source that fills all of space, that energy would, like the hidden
motors, keep the machine going, even though we could not detect the free
energy source by any other experimental means. In effect, the machine itself
would be the "free energy detector". They remind us that physicists once
ridiculed the idea of energy stored in atoms. Yes, they did, as these quotes
indicate.
There is no likelihood man can ever tap the power of the atom. The glib
supposition of utilizing atomic energy when our coal has run out is a completely
unscientific Utopian dream, a childish bug-a-boo. Nature has introduced a
few fool-proof devices into the great majority of elements that constitute
the bulk of the world, and they have no energy to give up in the process
of disintegration.
- Robert A. Millikan (1863-1953) [1928 speech to the Chemists' Club (New
York)]
...any one who expects a source of power from the transformation of these
atoms is talking moonshine...
- Ernest Rutherford (1871-1937) [1933]
So, do the "free-energy" proponents have a valid point here? Are they justified
in devoting their time to seeking a "free-energy" or "over-unity" systems?
Should mainstream scientists take up such research to solve our energy problems?
I think not. Scientists generally pursue something only when there's clear
evidence pointing to a need for extending, clarifying or otherwise changing physical theory. So
far, not one scrap of credible or even suggestive evidence for the existence
of this "free-energy" has been seen. To return to the comparison with atomic
energy, the initial skepticism of Millikan, Rutherford, and Einstein was
well justified. But they changed their opinions as new evidence came in.
Their initial skepticism did not in any way retard our progress toward discovery
and utilization of atomic energy. My hunch is that if there is anything like
"free-energy" anywhere in the universe, it will not be discovered by the
kind of people now making wild and unfounded claims about it, nor by the
methods they are using to try to tap it. It helps to have evidence for,
and know something about,
a source of energy before one attempts to figure out how to utilize it. All
the ingenuity in the world can't extract energy from something that isn't there, has no energy to extract, or no way to convert it to useful work.
The production of useful work is strictly limited
by the laws of thermodynamics, but the production of useless work seems to
be unlimited.
—Donald Simanek |
|
What about possible "accidental" discovery of free energy by some basement
PM tinkerer? Weren't X-rays discovered accidentally, when no one even suspected
their existence and certainly had no idea what they were? Yes, that's one
of the (very few) examples of a truly accidental important discovery in physics.
Quite a number of people stumbled on evidence for X-rays before Röntgen
but failed to follow up with experiments to see what was going on.
Anti-serendipity? But during that same period of history we have the interesting
phenomena of other people "discovering" things that did not exist,
such as N-rays, and later M-rays (mitogenetic radiation). So in which category
will "free energy" fall, if and when someone claims to have found experimental evidence for it? Only time will tell.
On the whole, scientific discoveries, even accidental ones, are most likely
to be made, investigated, and exploited by folks who have a very good
understanding of the relevant principles of existing science. Ignorance of
well established science causes many sincere and dedicated people to waste
lives and careers chasing moonbeams. The sincere PM proposals of the past
illustrate the fact that their inventors did not have sufficient understanding.
Many of them believed that such understanding wasn't necessary,
or they rejected it out of hand.
Top
Buoyancy motor #1
John Phin describes
this one in his classic book Seven Follies of Science (Van Nostrand,
1906), attributing it to a correspondent named "Power".
A J-shaped tube A, Fig. 14, is open at both ends but tapers at the lower
end, as shown. A well-greased cotton rope C passes over the wheel B and through
the small opening of the tube with little or no friction, and also without
leakage. The tube is then filled with water. The rope above the line WX balances
over the pulley, and so does that below the line YZ. The rope in the tube
between these lines is lifted by the water, while the rope on the other side
of the pulley between these lines is pulled downward by gravity.
Phin says that the "inventor offers this device as a kind of puzzle rather
than as a sober attempt to solve the famous problem," and Phin concludes by
asking why it will not work.
As usual, Phin misses the point (and the fun) of the challenge in his analysis
of this puzzle. He trots out the usual lame dismissals such as bearing friction,
work required to bend the rope, and friction of the rope at the water-seals,
then, supposing the case is closed, moves on to something else.
I rephrase the
challenge, and show a simpler picture. The smooth rope passes through a container
of liquid, with an impermeable frictionless seal in the bottom.
I also set a ground rule to deflect irrelevant responses: Assume everything
is perfect. No friction, leakless seals, perfectly flexible impermeable rope,
no viscous drag between rope and liquid. Even with these ideal conditions
we can easily and simply show that this machine will not work as claimed.
Why did the inventor of this problem think it should seduce us into thinking
it might work? It's his phrase "lifted by the water". He is, of course referring
to the buoyant force of Archimedes' principle: "A body immersed in liquid
experiences and upward buoyant force equal to the weight of the displaced
liquid." This principle is found in every elementary physics textbook, but
seldom understood by students. They use it blindly, not knowing why it is
true nor under what conditions it is true, and they haven't paid attention
to how it is derived.
The claim is that the upward buoyant force on the portion of the rope in
the liquid causes the rope to move upward there. This claim is false. Why?
Answer:
There is no buoyant force on the rope. This deception is a based on a common
misunderstanding of Archimedes' principle. The principle requires that the
submerged body have liquid beneath it so that the net force due to the liquid
acting on the body has nonzero upward component. The principle also works
if a body is totally immersed, with water above and below, or floating, with
water only below. After all, what is the source of the buoyant force?
It is the pressure difference between upper and lower surfaces. Consider
a totally immersed cylinder with its axis vertical (very appropriate in this
case). Pressure on the sides of the cylinder provides only horizontal forces
that also add to zero, and more importantly, have no vertical components.
Only forces due to pressure on top and bottom surfaces have vertical components.
The pressure on the bottom is greater than that on top by amount
r gh, where r
is the liquid density. So there's a net upward
force on the cylinder.
In this PM puzzle, there's no liquid above or below the rope capable of providing
an upward component of force. All the forces on the rope due to the liquid
are strictly horizontal, and because these forces are symmetrically distributed
around the circumference of the rope, they add to zero.
An astute correspondent notes that my argument here lacks generality. He
proposes a variant in which the rope passes through the liquid at an angle,
say making an angle of 45° to the vertical. Now there is liquid
above and below the rope. And if there's now a buoyant force on the rope,
it surely has an upward component in the direction of the rope, and therefore
this version of the machine should work. Why doesn't it?
Solution left as exercise for the student. The solution might require
calculus. Here's a helpful hint. That Buoyant force mentioned in Archimedes'
principle is not some new "magic" force that arises when a body is immersed.
The buoyant force is a resultant (sum) of pressure forces acting on the immersed
body. Archimedes' principle is merely an expression of a useful relation
between the densities of the bodies involved, resulting from geometric laws
and the fact that pressure exerts force normal to a surface.
Top
Buoyancy motor #2
Here's yet
another PM machine claiming support in Archimedes' principle. Poor misunderstood
Archie really takes a beating.
Claim:
A wheel in the form of a perfect sphere or cylinder rotates about a frictionless
horizontal shaft. The left side is in a chamber filled with water, perfect
(frictionless and leak-proof) seals around the rotating wheel prevent the
liquid from escaping. The left side of the wheel therefore experiences an
upward buoyant force due to the liquid it displaces. So that side will rise,
and the wheel rotates clockwise.
Answer:
All forces exerted by the liquid upon the circumference of the wheel
are normal to the wheel's surface, and therefore pass through the wheel's
rotation axis. All of these forces have zero lever arm with respect to this
axis. The liquid therefore provides no torque about the wheel axis and the
wheel won't turn.
| Be skeptical of any cyclic perpetual-motion
proposal that can be operated equally well in either direction. |
|
Stevin's principle of virtual work demolishes this PM device neatly. We know
the wheel will have no tendency to rotate because if we imagine a virtual
displacement of the wheel through any angle, the system would still be just
the way it was before, with no change in its energy and no change in
configuration. No work is done in the process.
Richard G. Clegg's
Perpetual
Motion Page has a clever variant of this buoyant motor. Instead of a
wheel it has a torus (doughnut-shaped ring) passing through two seals separating
two chambers having liquids of different density. There is no axle. One half
of the ring is surrounded by liquid, inside and outside. The seals are of
course frictionless and leak-proof. There's no axle to provide reaction forces.
Here the forces on the ring due to pressure do have upward components. Why
won't this one work? [Picture used with permission of Richard G. Clegg.]
Answer left as exercise for the student.
Top
Buoyancy motor #3
This perpetual
motion machine probably dates from the mid 1800's. The main drum is filled
with a liquid. In it are round chambers filled with air (or a vacuum) and
connected by rods to the weights outside. The rods slide in frictionless
leak-proof seals, of course. As with many such proposed mechanisms, this picture
is more complicated than necessary to illustrate the principle upon which
it is supposed to work. The drawings below show just one weight and one air
chamber immersed in liquid.
When in position 1, the buoyancy of the lower sphere is enough to lift the
weight to its highest position. If the drum is now pushed so it moves counter
clockwise, the weight stays at this large radial distance at least until
it has rotated 90°.
During the next quarter turn the weight has a large lever arm. At the end
of this quarter turn, position 3, the air chamber rises to the top of the
drum, and the weight is now is at its smallest radial distance, (and smallest
lever arm) where it stays for the next quarter turn. During the last quarter
turn the air chamber's buoyancy causes the weight to rise until it is at
its largest radius.
Since the torque during the second quarter turn is greater than during the
third quarter turn, the wheel will gain more energy there than it needs to
move upward during the fourth quarter-turn.
The principles that are supposed to make this thing work allow the machine
to be started by a push in either direction, and it would work just as well
clockwise as counterclockwise. That's a bit suspicious, isn't it? Also, if
we imagine motion of this wheel through a full cycle, the final and initial
states are indistinguishable, so Stevin's principle tells us that it won't
turn. Yet we'd still like to analyze the details to see exactly where the
inventor went astray.
We'll give you a grant to buy frictionless bearings, a liquid with zero
viscosity, and leak-proof frictionless seals for the movable rods. With all
of this advantage, why will it still not work?
Solution by Ben Mitch.
Top
Buoyancy motor #4
Here's a new addition to our museum, contributed by Dave Carvell. This one
has some innovative details to challenge your understanding of physics.
The sealed
container has two vertical tubes. The right one contains a liquid (cyan)
such as water, and a very light ball (red), much lighter than the liquid.
As usual we'll let you use a liquid with zero viscosity. (We are generous
about these details that don't matter anyway.)
Two "gates" G1 and G2 are made like iris diaphragms that can open and close
quickly. They are, of course, watertight when closed.
Now we all know that when a light object, like a cork, is underwater, then
released, it pops to the surface and can even pop above the surface. We take
advantage of that fact. Our machine, with its viscosity-free liquid, should
allow even greater speed at the top. The machine is started with the ball
at the bottom. As it rises, a high-tech sensor quickly opens gate G1 to let
it through, closing the gate immediately, and then opening gate G2
in time for the ball to pass through.
Since one of the gates is closed at all times the water levels are maintained.
The ball pops above the surface with some momentum, and the curved top of
the apparatus deflects it to the other tube, where it falls, gaining speed
and momentum in the fall, enough so that it goes under the liquid surface
there and is bumped over into the right tube, where, of course, it begins
to rise. This should go on forever, gaining speed each cycle.
Surface tension and viscosity present real problems here. But before we go
to the trouble to find a perfect fluid for this device, we should look for
even more fundamental flaws.
Solution
Top
Capillary motor
Claim:
This is one of my favorite PM proposals for challenging student understanding.
Most students know that liquids will rise in a very narrow tube, the process
being called "capillary action". Suppose we have such a tube capable of lifting
the liquid to a height h. Now lower the tube to a height less than
h. Or make a hole in its side below the top of the liquid column.
The liquid, trying to rise to height h will then spill out the top
of the tube, where a very tiny waterwheel can capture its energy as it falls.
Answer:
This is only likely to fool
people who haven't considered why capillary action occurs. The usual
textbook diagram is shown at the left. Surface tension acts at the liquid
surface where it contacts the walls of the tube. These intermolecular forces
between liquid and glass are greater than those between the liquid molecules
themselves. This gives rise to a curved "meniscus" shape of the upper liquid
surface. The forces around this interface act at an angle with a significant
upward component that can hold the water column in static equilibrium.
The pressure of the water at the surface of the reservoir is atmospheric pressure,
both outside and inside the capillary tube. This is due to Pascal's principle
that the pressure at all points at a given height within a liquid is the same.
Also, by the same principle, the pressure within the capillary tube, just below the meniscus,
is less than atmospheric pressure by amount rgh.
This accounts for the pressure difference across the meniscus that in turn accounts for
its shape. The atmosphere is pushing down on the meniscus, but molecular adhesion forces
around its edge oppose that. It acts like an elastic sheet restrained at its edges.
If one now gradually lowers the tube, the supported column of liquid remains the same length. The top of the tube moves down to meet the meniscus. Continue to lower the tube and finally the liquid column reaches the top of the tube. But, remember, the pressure just below the meniscus is still lower than atmospheric pressure, so the meniscus still bulges downward. It does not spill over the top of the tube. The liquid surface always contacts
the upper rim of the tube, and as the tube is lowered even more, the meniscus follows
it down.
This picture
shows situations you might have imagined possible. The version
shown in the second figure, with a hole in the side, is easily discredited. The hole
must be smaller than the tube diameter, so it, too will exhibit surface tension
forces. The pressure just inside this hole is still lower than atmospheric pressure, so the water will bulge inward, not outward, and no liquid will pass through it.
Pressure increases downward in a liquid, by the law
ρgh where ρ is the liquid density. The pressure at the
liquid surface outside the capillary tube is atmospheric. So the pressure
within the tube must decrease with height up to the meniscus. It's the pressure
difference across the meniscus that is responsible for its curved shape.
The second figure depicts an outcome that just can't happen.
Top
Capillary wheels
Claim:
This idea appeared in the correspondence column of the
April 22, 1911 issue of Scientific American.
The editor invited readers to "search out the fallacy of this ingenious device."
Imagine two very carefully machined wheels with parallel axes on frictionless
bearings. They are partly immersed in a liquid. There's a very narrow
space between the flat portions of the wheels, causing liquid to be drawn
up between, by capillary action. The weight of this sheet of liquid exerts
downward forces on both wheels; therefore they should rotate in opposite
directions as shown by the arrows. Since the force is small, the speed will
be low also, giving the capillary column plenty of time to rise to compensate
for this motion, maintaining a steady height.
As usual, ignore
friction and viscosity. The column of liquid is certainly being supported
by an upward force provided by the wheels. Newton's third law requires that
the column of liquid exerts a downward force on the wheels. This surely provides
a torque on both wheels. So why don't they move?
Another version, using pulleys and belts is shown at the left. The principle
is the same, so we expect this to work just as well as the wheel version.
This is another case where indistinguishable initial and final states and
Stevin's principle should have aborted this project at the conceptual stage.
Answer and discussion.
Top
George Sinclair's siphon.
This curious
device appears in a 1669 book on pneumatics (in Latin) by philosophy professor
George Sinclair of Glasgow University. Dircks mentions it in his 1870 book
Perpetuum Mobile (p. 42) from which we took this picture.
Apparently the upper bulb has reduced pressure of air within it, sustaining
the liquid drawn up from the dish. One end of a siphon transfers liquid from
this bulb up through the bent rod and back to the dish. This loss of liquid
from the bulb is replaced by more liquid drawn from the dish, due to the
low air pressure in the bulb. Result: an endless circulation of liquid. A
little water wheel might be run by the water exiting from the siphon into
the dish. Well, maybe not.
Sinclair must have thought this device pretty neat, for he devoted 18 pages
to discussion of its merits. You, dear reader, should easily demolish it
in a few paragraphs.
Answer and discussion.
Top
Bob Schadewald's gravity engine.
Artist's conception of the gravity engine power station. The engine is
an overbalanced wheel or off-axis weight with (of course) frictionless bearings.
Based on the assumption that the universal gravitational constant is continually
decreasing this engine exploits the small energy that can be gained from
this during each revolution. In keeping with the philosophy of the engine
itself, power is transferred to the electric generator by a linkage of devious
pulleys and belts. [Drawing © 1992 by Donald E. Simanek.]
First, let's be very clear that Bob's BS Gravity
Engine is a parody, a joke. His intent was to tease, and amuse, and to
tweak physicists and engineers whose understanding of physics was shaky.
It was a challenge to readers to show conclusively whether or not it could
work, given the "decreasing gravity" assumption. He was careful never to
fully answer that question or to explain the joke.
The suggestion that the universal gravitational constant might be declining
came out of speculative theoretical work of Paul A. M. Dirac. In 1937 he
suggested that the universal gravitational constant G might be
weakening, proportional to the age of the universe. He even predicted that
in 10 billion years it might be only half what it is today. Since then the
notion that fundamental constants, including the speed of light, might change
over time has fascinated speculative theorists. It has also fascinated new-age
wackos, who shamelessly adapt and pervert the idea to fit their own agendas.
Obviously the BS engine falls into my class (2) and possibly (4).
Stevin's principle does not kill this proposal, for the initial and final
states of the system (including its environment) after each cycle are not
identical. This wheel would operate equally well in either direction, however,
that is always suspicious.
Scott Morris discussed some PM machines in OMNI magazine in 1990 (July, p.
98 and 99; August p. ?), and quotes Bob Schadewald as saying "My description
is a subtle deception. The velocity of the moving weight will never exceed
what it was when it passed the bottom, dead center, the first time, even
if there is no friction. The weight may pick up speed at the top, but never
at the bottom, so there is never any real speedup in the wheel."
How does Bob arrive at that conclusion? Can this unexpected result be justified
by elementary physics? And why does Bob say "the weight may pick
up speed at the top, but never at the bottom"?
Answer and discussion.
Top
Simanek's bouncing ball engine
This PM proposal works just as well at Bob Schadewald's Gravity Engine (SGE)
and it may be easier to analyze. Doing so might shed some light on the
principles behind the SGE.
Bob cast his SGE in the form of a wheel. This introduces the feature of rotation
that is a "red herring" for some people. They think that the paradox somehow
depends on rotation or requires consideration of centrifugal effects. It
doesn't, as this non-rotating bouncing ball engine illustrates.
Inventor reads by light powered by
electricity provided by the ceiling transducer of
a bouncing ball engine. He's wearing earplugs.
A ball bounces up and down between floor and ceiling, both rigid and massive.
The bounces are assumed elastic, that is, the ball's velocity after impact
is the same as before impact, but with reversed direction.
Now imagine that the gravitational constant g is slowly but steadily
decreasing. The ball is released at rest from the ceiling. The ball attains
a certain speed when it reaches the floor, and rebounds with that same speed.
But since g is now smaller, the ball still has a small velocity
when it hits the ceiling. Clearly this means that on completion of this
ceiling-to-floor-to-ceiling cycle it has gained a small amount of kinetic
energy, which we could extract with a slightly inelastic ceiling panel. The
panel would steal just that extra amount of energy, bringing the ball to
rest there momentarily. The ball would then start the next cycle with zero
speed, as in the previous cycle. The gravitational force, though slightly
smaller than before, would cause the ball to fall to the floor and bounce
back to the ceiling, where we again steal the excess energy gained in this
cycle, and so on forever, or until gravity runs out, whichever comes first.
The assumptions of perfectly elastic impact and infinite mass floor are no
more unreasonable in posing this apparent paradox than the assumption of
frictionless bearings in the wheel. Given these assumptions we still ought
to be able to analyze the machine and show whether it could work as claimed.
Answer and discussion.
Top
The Gravity shield engine
Claim:
This proposal is at least a century old. Classic simplicity! A wheel has
a frictionless axle. Now just insert a gravity shield under one side, making
that side lighter and this will initiate and maintain rotation. Indeed, you'd
better extract energy from it continually, or put a brake on it, or it will
spin so fast it will tear itself apart.
I've often seen this without reference to its inventor. If anyone knows who the inventor is, please let me know. Nicola Tesla described it,
in his article "The Problem of Increasing Human Energy" in Century Illustrated Magazine, June 1900.
It is possible, and even probable, that there will be, in time, other resources of energy opened up, of which we have no knowledge now. We may even find ways of applying forces such as magnetism or gravity for driving machinery without using any other means. Such realizations, though highly improbable, are not impossible. An example will best convey an idea of what we can hope to attain and what we can never attain. Imagine a disk of some homogeneous material turned perfectly true and arranged to turn in frictionless bearings on a horizontal shaft above the ground. This disk, being under the above conditions perfectly balanced, would rest in any position. Now, it is possible that we may learn how to make such a disk rotate continuously and perform work by the force of gravity without any further effort on our part; but it is perfectly impossible for the disk to turn and to do work without any force from the outside. If it could do so, it would be what is designated scientifically as a "perpetuum mobile," a machine creating its own motive power. To make the disk rotate by the force of gravity we have only to invent a screen against this force. By such a screen we could prevent this force from acting on one half of the disk, and the rotation of the latter would follow. At least, we cannot deny such a possibility until we know exactly the nature of the force of gravity. Suppose that this force were due to a movement comparable to that of a stream of air passing from above toward the center of the earth. The effect of such a stream upon both halves of the disk would be equal, and the latter would not rotate ordinarily; but if one half should be guarded by a plate arresting the movement, then it would turn.
Critics will be quick to observe that if one imagines a virtual rotation
through a small angle, the wheel is physically the same as before. The small
portion at the bottom that was in the gravitational field becomes weightless
over the gravity shield, but at the same time an equal segment of the wheel
moves from weightless condition back into the gravitational field. They therefore
argue that nothing has changed, and there is no reason there should be such
motion. This is a nice application of Stevin's principle of virtual work.
The unknown inventor might argue thusly: Remove the gravity shield. Imagine an equivalent:
a half-wheel. It would rotate under the action of gravity and then continue
to swing like a pendulum. You can hardly deny that if one half of the wheel
suddenly had no gravitational force upon it, the other half would move due
to the unbalanced torque.
This suggests
a better design. Don't use a wheel. Use an unbalanced weight as in the SGE
(see previous item). Start the machine with the weight at the top of its
range. Give it a slight nudge toward the unshielded side, and it will fall,
gaining kinetic energy. This kinetic energy at the bottom remains unchanged
during its upward motion over the shield, and is still there when the weight
reaches the top, carrying it into the unshielded side where it picks up still
more energy, and so on forever. What prevents that?
There's always the possibility that you may assume some part of the machine
that is itself physically impossible. If one too readily grants its possibility,
much time can be wasted analyzing the other parts of the machine. Here the
suspect part is the gravity shield. Can we simply and conclusively show that
a gravity shield is or is not possible? Can we show that its very existence
would violate some fundamental law?
This puzzle doesn't require a perfect shield. A shield that reduces the
gravitational force by only a few percent would seem to meet the requirements
of a perpetual motion machine. We need to show, by simple physics that (1)
the very existence of such a shield would violate fundamental laws of physics,
or (2) even with such a shield, the wheel would not turn perpetually and
would not gain speed or (3) some fundamental law of physics is wrong, and
so is Stevin's principle and the laws of thermodynamics.
The rationale for this wheel says that it will only gain speed in one direction.
If turned in the other direction it would lose speed. This may be a clue.
Stevin's principle demolishes the version with a uniform wheel, for the initial
and final states of the system and environment are identical for any virtual
displacement of the wheel. Therefore the wheel cannot move on its own. So
why did we mistakenly think that it should turn by itself? Stevin's
principle also discredits the eccentric weight version, for a virtual
displacement of one revolution returns the wheel an identical state. But that
doesn't help us understand what's going on during each cycle.
Discussion and answer.
Top
The Classic magnetic shield engine
A reader informs us that a device of this sort was given as an extra credit
homework problem by an MIT professor back in 1985.
Chris Cheng, a high school student from Sydney, Australia, sent us a simple
version, from which this one evolved through a process of tinkering.
How it's supposed to work.
Magnetic shielding materials are available. They aren't perfect shields,
but for the purposes of this motor they don't need to be perfect.
A freely rotatable armature in the center consists of a permanent magnet
partly covered with a magnetic shield (solid black). The shield has openings
at the right, near the poles. An outer ring has magnets in a radial array
with their north poles inside, firmly fastened to a rigid frame. These magnets
are long, so the south poles are at a considerably greater radius than the
north poles. The magnetic field from a magnet pole decreases in strength
with distance.
The shield apertures permit each armature pole to "see" only a couple of
the magnets of the outer ring. Each armature pole is affected primarily by
the north poles of the ring, those being nearest. Therefore, in the position
shown in the picture, the N pole of the armature is repelled, experiencing
a force to the left. The S pole of the armature is attracted, experiencing
a force to the right. These two forces make a couple, which rotates the armature
clockwise.
Classic simplicity! If you wanted to improve it, those outer magnets could
be swung up or down so they were in a cylindrical array of magnets with their
axes parallel. Then a similar armature could be placed in the plane of the
S poles, operating on the same axle as the armature in the plane of the N
poles. This should double the power output!
We caution the reader that this machine has details that could be subtle
and difficult to analyze in detail. Gauss's and Stokes' laws in vector calculus
form may be required for a full analysis. However, this machine has a simple
and fundamental flaw that can be appreciated even at the introductory physics
level.
Answer and discussion.
Top
Re: Answers left as exercise for the student. Send your answers to the address
shown at the right. The
earliest good answer(s) that arrive may be posted here, with credit to author.
I will post (at my discretion) answers that are simple to explain, clear,
correct, perceptive, and that stimulate thinking and further discussion.
Posted answers, whether written by me or by others, do not always represent
the final word on a given proposal. On several occasions perceptive readers
have noticed things we missed, or suggested simpler ways to explain something.
So don't hesitate to skeptically rethink given "answers".
While I welcome submission of new or innovative perpetual motion puzzles,
I assume no obligation to respond in detail to all of them. In particular,
I cannot be expected to analyze vague proposals, overly and
unnecessarily
complicated designs, nor ideas that are simply variations of classics found
in the literature. I've already received proposals that fail for the same
reasons already discussed above, indicating that the person proposing the
idea hadn't fully understood this document. Also, I choose not to include
devices that would require advanced mathematics or physics for detailed
analysis. I don't like to post puzzles unless I am reasonably confident what
the flaw is, and that the flaw can be explained using elementary physics
principles.
To those inventors whose creations I choose not to include in the museum
collection, I offer this comment and consolation:
"It may be perpetual motion, but it will take forever to test it."
Cartoon by Donald Simanek.
Top
Links
Top
References and additional reading:
When I first became interested in this subject, most of these references were rare, hard to find books. I was fortunate to have copies of them. Now [2012] many of them are available as free ebooks. Others are available in expensive reprint editions. There's now no excuse for any hopeful perpetual motion machine inventor to be ignorant of the long history of this subject.
-
Angrist, Stanley W. "Perpetual Motion Machines" in Scientific American,
Jan 1968. This article is also in a Sci. Amer. reprint book.
-
Angrist, Stanley W. and Loren G. Hepler. Order and Chaos. Basic Books,
1967. [QC311.A5]
-
Collins, John. Perpetual Motion: An Ancient Mystery Solved?
Permo Publications, 1997, 2005.
A history of Johann Bessler, compiled from original sources.
-
Dircks, Henry. (1806-1873) Perpetuum Mobile, or the search for self-motive
power during the 17th 18th and 19th centuries. London, E. & F. Spon,
16 Bucklersbury, 1861. Rogers and Hall Co., 1916.
-
Dircks, Henry. (1806-1873) Perpetuum Mobile, or the history of the search
for self-motive power from the 13th to the 19th century. London, E. &
F. Spon, 48 Charing Cross, 1870.
-
Dircks, Henry. (1806-1873) Scientific Studies or Practical, in Contrast
With Chimerical Pursuits, Exemplified in Two Popular Lectures. I. The Life
of Edward Somerset, Second Marquis of Worcester, Inventor of the Steam Engine.
II. Chimeras of Science: Astrology, Alchemy, Squaring the Circle, Perpetuum
Mobile, Etc. London, E. & F. N. Spon, 48 Charing Cross, S. W. 1869.
-
Gardner, Martin Fads and Fallacies in the Name of Science. Dover, 1952, 1957. This is a classic. This book has no chapter on perpetual motion, but Gardner's comments on the psychology of pseudoscientists and cranks apply equally well to many perpetual motionists. See the next reference for his comments on perpetual motion.
-
Gardner, Martin. Perpetual Motion: Illusion and Reality, Foote Prints,
(house magazine of Foote Mineral Co., Exton, Pennsylvania.) Vol. 47, No. 2, 1984, p. 21-35.
-
Herring, Daniel Webster (1850-1938). Foibles and Fallacies of Science. Van Nostrand, 1924.
-
Hiscox, Gardner D., M.E.
Mechanical Appliances and Novelties of Construction.
Normal W. Henley Publ. Co., 1927.
Chapter 23, available online, is a marvelous resource of about 60 failed mechanical devices, with pictures. Inventors' names, dates, and patent numbers are usually not given, nor does this source give reasons why the devices don't work. Hiscox's preamble suggests that scientific opinion is divided on the possibility of perpetual motion. But his description of many of these devices reveals that he has no doubt about their impossibility, and he seems to be saying "Of course you can see why these obviously won't work, so I don't need to spell it out." Alas, that
is not at all obvious to many inventors, even today, who peddle minor variations of these old and discredited ideas, fully confident that they must work. If you have just invented a seemingly marvelous perpetual motion machine, you'd better look here to see whether it has been done before. If it has, you can be sure it doesn't work.
-
Jastrow, Joseph. The Story of Human Error. D. Appleton-Century Company, 1936. Chapter on "Error in Physics," by W. F. G. Swann. Books for Libraries.
-
Moore, Clara Bloomfield. Keely and His Discoveries. (Reprint ed with foreword by Leslie Shepard, University Books, 1972?. Original edition, 1893(?).)
Mrs. Moore was one of Keely's most faithful supporters. Keely's explanations of his theories were incomprehensible even to those sympathetic to his work, and this book provides many examples of this.
-
Ord-Hume, Arthur W. J. G. Perpetual Motion. St Martins Press, 1978. Ord-Hume was an engineer who wrote extensively on antique clocks and other mechanisms. But his cavalier "refutations" of many of the perpetual motion machines are trivial and misleading. Some parts, particularly chapter 6, are difficult to follow. But, the book has the virtue of still being in print, in paperback, and as a historical survey of the subject it is well worth owning. However, the drawings in the Barnes and Noble reprint edition are poorly reproduced. Several internet sources have this as a free e-book, but some of the illustrations are poorly reproduced.
-
Phin, John. The Seven Follies of Science. D. Van Nostrand, 1906. The line drawings are very clearly reproduced, apparently redrawn from original sources. The explanations often miss the mark.
-
Scientific American, 1884, has references to J. W. Keely, generally derogatory and even sarcastic. March 19, p. 196. April 5, p. 213. Oct 11, p. 230. These are free online.
-
The Scientific American Supplement has seven lengthy articles about perpetual motion machines, described in detail, with nice engravings, and wry sarcasm as well. This is a free download from Google.
-
Verance, Percy (Pseudonym!). Perpetual Motion. 20th Century Enlightenment Specialty Co., 1916. This is material from Dircks'
books, reworked and condensed "for the general reader", and has many of the original illustrations. It is apparently a Rosicrucian publication, part of a series called: History, Explanation and Prophecy Illustrated. Warning: The clever pseudonym has been appropriated by several people recently, who have no connection with the anonymous author of this book.
A readable account of the Bessler story is found in:
-
Gould, Rupert. Oddities, A Book of Unexplained Facts.
1928, 1944, 1964, University Books 1965. Chapter V, Orffyreus' Wheel.
Some textbooks mention perpetual motion machines, or pose problems about
them.
-
Gettys, W. Edward, Keller and Skove. Classical and Modern Physics,
McGraw-Hill, 1989. End of chapter problems about the Escher "Waterfall" (p.
347), buoyant force paradox (p. 348), and the weighted piston device (p.
348).
-
Hudson, Alvin and Rex Nelson. University Physics, Harcourt Brace
Jovanovich, Inc. 1982. Section 21.7 discusses perpetual motion devices, with
pictures of an overbalanced wheel, a buoyancy motor, the 1618 closed-cycle
mill, the ammonia engine, and a picture of the Escher waterfall, all on p.
511.
-
O'Hanian, Hans C. Physics, W. W. Norton, 1985. Short description of
the two kinds of perpetual motion machines, with a drawing of the
articulated-hammer overbalanced wheel (p. 508).
Input and suggestions are welcome at the email address shown here.
When responding to anything on these web
pages please indicate the specific document by subject, name or filename.
All material in this museum is © 2002, 2003, 2020 by Donald E. Simanek,
with the exception of text and materials indicated as from
other sources. Latest revision, Jan 2016.
Return to front page.
Return to Bob Schadewald's corner.
Return to the top of this document.
![[NEW]](../new-helv.gif){kind=small}
Fake Perpetual Motion Machines You Can Build.
